题目内容
7.用列举法表示集合{x∈N|x-1≤2}为( )| A. | {0,1,2,3} | B. | {1,2,3} | C. | {0,1,2,3,4} | D. | {1,2,3,4} |
分析 根据题意,分析可得集合{x∈N|x≤3}的元素为小于等于3的全部正整数,列举法表示该集合即可得答案.
解答 解:集合{x∈N|x-1≤2}={x∈N|x≤3}的元素为不大于3的全部非负整数,
则{x∈N|x≤3}={0,1,2,3};
故选A.
点评 本题考查集合的表示方法,要灵活掌握集合的表示方法.

练习册系列答案
相关题目
17.不等式kx2-kx+1>0对一切实数x均成立,则k的取值范围是( )
| A. | 0<k<4 | B. | 0≤k<4 | C. | 0<k≤4 | D. | 0≤k≤4 |
18.已知A(3,0),B(0,4),△AOB绕y轴旋转一周得到的几何体的表面积和体积分别是( )
| A. | 9π,12π | B. | 12π,9π | C. | 24π,12π | D. | 15π,36π |
2.设实数x,y满足条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为 12,则$\frac{3}{a}$+$\frac{4}{b}$的最小值为( )
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
16.设点P是椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$上的一点,M、N分别是两圆:(x+3)2+y2=1和(x-3)2+y2=1上的点,则|PM|+|PN|的最大值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
8.在(2x+a)5的展开式中,含x2项的系数等于320,则$\int_0^a{({e^x}+2x)dx}$等于( )
| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
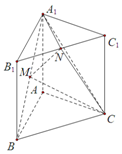 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.