题目内容
下列说法中,正确的是( )
| A、命题“若a<b,则am2<bm2”的逆命题是真命题 |
| B、“p∧¬q为真命题”是“q为假命题”成立的充分不必要条件 |
| C、命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x<0” |
| D、已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:A.写出原命题的逆命题,然后加以判断,注意m可为复数;B.先根据复合命题的真假,判断p,q,然后由充分必要条件的定义加以判断;C.由存在性命题的否定形式加以判断;D.根据充分必要条件的定义加以判断.
解答:
解:A.“若a<b,则am2<bm2”的逆命题是“若am2<bm2,则a<b”显然m为复数i,得a>b,故是假命题,故A不正确;
B.若p∧¬q为真命题,则p,¬q均为真命题,即q为假命题,若q为假命题,则p∧¬q不一定为真命题,故B正确;
C.由命题的否定方法得:命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x≤0”,故C不正确;
D.已知x∈R,.x>1不能推出x>2,但x>2可推出x>1,故“x>1”是“x>2”的必要不充分条件,故D不正确.
故选:B.
B.若p∧¬q为真命题,则p,¬q均为真命题,即q为假命题,若q为假命题,则p∧¬q不一定为真命题,故B正确;
C.由命题的否定方法得:命题“存在x∈R,x2-x>0”的否定是“对任意x∈R,x2-x≤0”,故C不正确;
D.已知x∈R,.x>1不能推出x>2,但x>2可推出x>1,故“x>1”是“x>2”的必要不充分条件,故D不正确.
故选:B.
点评:本题考查简易逻辑的基础知识:四种命题及真假,充分必要条件,复合命题的真假,以及命题的否定,注意与否命题加以区别,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知中心在坐标原点,焦点在坐标轴上的双曲线的渐近线方程为y=±
x则该双曲线的离心率为( )
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
C是以原点O为中心,焦点在y轴上的等轴双曲线在第一象限部分,曲线C在点P处的切线分别交该双曲线的两条渐近线于A,B两点,则( )
A、|OP|<
| ||
| B、|OP|=|AB| | ||
C、
| ||
D、|OP|=
|
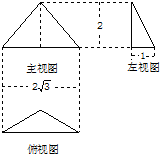 已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|