题目内容
8.若实数x,y满足不等式$\left\{\begin{array}{l}{x+y<2}\\{x>0}\\{y>1}\end{array}\right.$,则目标函数z=x-y的取值范围为(-2,0).分析 先根据约束条件画出可行域,再利用几何意义求最值,z=x-y表示直线在y轴上的截距的相反数,只需求出可行域直线在y轴上的截距的范围即可.
解答 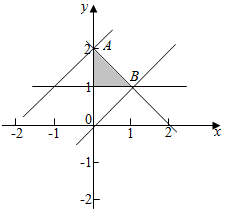 解:不等式组$\left\{\begin{array}{l}{x+y<2}\\{x>0}\\{y>1}\end{array}\right.$,表示的平面区域如图所示,
解:不等式组$\left\{\begin{array}{l}{x+y<2}\\{x>0}\\{y>1}\end{array}\right.$,表示的平面区域如图所示,
当直线z=x-y过点A(0,2)时,
在y轴上截距最大,此时z取得最小值-2.
当直线z=x-y过点B(1,1)时,
在y轴上截距最小,此时z取得最大值0.
目标函数z=x-y的取值范围为(-2,0)
故答案为:(-2,0).
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.对于椭圆${C_{(a,b)}}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a,b>0,a≠b)$.若点(x0,y0)满足$\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}<1$.则称该点在椭圆C(a,b)内,在平面直角坐标系中,若点A在过点(2,1)的任意椭圆C(a,b)内或椭圆C(a,b)上,则满足条件的点A构成的图形为( )
| A. | 三角形及其内部 | B. | 矩形及其内部 | C. | 圆及其内部 | D. | 椭圆及其内部 |
16.如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=90°,侧面PAB⊥底面ABC,AB=PA=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
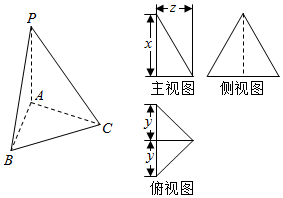

| A. | $2\sqrt{3}$,$2\sqrt{2}$,2 | B. | 4,2,$2\sqrt{2}$ | C. | $2\sqrt{3}$,2,2 | D. | $2\sqrt{3}$,2,$2\sqrt{2}$ |
20.已知数列{an}是公差为$\frac{1}{2}$的等差数列,Sn为{an}的前n项和,若S8=4S4,则a8=( )
| A. | 7 | B. | $\frac{9}{2}$ | C. | 10 | D. | $\frac{15}{4}$ |