题目内容
6.任取x,y∈[0,1],则点(x,y)落在抛物线y2=x和x2=y围成的封闭区域内的概率为$\frac{1}{3}$.分析 根据几何概型的概率公式结合积分的应用求出对应区域的面积,进行求解即可得到结论.
解答 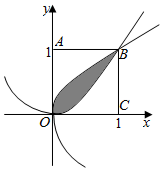 解:由y2=x得y=$\sqrt{x}$,(y≥0).
解:由y2=x得y=$\sqrt{x}$,(y≥0).
由y2=x和x2=y得交点B(1,1),
则阴影部分的面积S=∫${\;}_{0}^{1}$($\sqrt{x}$-x2)dx=($\frac{2}{3}$x${\;}^{\frac{3}{2}}$-$\frac{1}{3}$x3)|${\;}_{0}^{1}$=$\frac{2}{3}$-$\frac{1}{3}$=$\frac{1}{3}$,
故答案为$\frac{1}{3}$,
点评 本题主要考查几何概型的概率的计算,根据积分的应用求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
16.如图,已知三棱锥P-ABC的底面是等腰直角三角形,且∠ACB=90°,侧面PAB⊥底面ABC,AB=PA=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
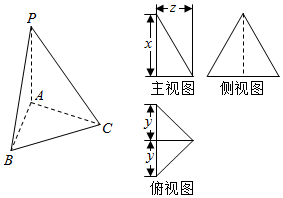

| A. | $2\sqrt{3}$,$2\sqrt{2}$,2 | B. | 4,2,$2\sqrt{2}$ | C. | $2\sqrt{3}$,2,2 | D. | $2\sqrt{3}$,2,$2\sqrt{2}$ |
14.已知函数$f(x)=\left\{\begin{array}{l}{x^3}\\ sinx\end{array}\right.$$\begin{array}{l}x≥0\\ x<0\end{array}$,则$f[f(-\frac{3π}{2})]$=( )
| A. | -sin1 | B. | sin1 | C. | -1 | D. | 1 |
1.设x,y满足约束条件$\left\{{\begin{array}{l}{x≥1}\\{x-2y≤0}\\{y-2≤0}\end{array}}\right.$,则z=x+2y-3的最大值为( )
| A. | 8 | B. | 5 | C. | 2 | D. | 1 |
11.复数$\frac{1}{{i}^{5}}$的虚部为( )
| A. | 1 | B. | -1 | C. | 0 | D. | -i |