题目内容
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,若cosA=
,a=
,c=2,求:
(1)sin2(B+C)+cos2A;
(2)b的值.
| 1 |
| 2 |
| 7 |
(1)sin2(B+C)+cos2A;
(2)b的值.
考点:余弦定理
专题:解三角形
分析:(1)由三角函数的平方关系结合已知求得sinA,然后展开倍角公式代值得答案;
(2)直接利用余弦定理求解b的值.
(2)直接利用余弦定理求解b的值.
解答:
解:(1)∵cosA=
,且A为△ABC的内角,则sinA=
,
∴sin2(B+C)+cos2A=sin2A+2cos2A-1
=
+2×
-1=
;
(2)由余弦定理得:a2=b2+c2-2bc•cosA,
则(
)2=b2+22-2×2b×
,解得:b=3.
| 1 |
| 2 |
| ||
| 2 |
∴sin2(B+C)+cos2A=sin2A+2cos2A-1
=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
(2)由余弦定理得:a2=b2+c2-2bc•cosA,
则(
| 7 |
| 1 |
| 2 |
点评:本题考查了三角函数的化简与求值,考查了余弦定理的应用,是中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
过圆x2+y2-6x-8y+21=0上一动点P作圆x2+y2=4的两条切线,切点分别为A、B,设向量
、
的夹角为θ,则cosθ的取值范围为( )
| PA |
| PB |
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
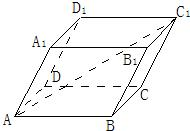 如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.
如图,在平行六面体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,AC1=5,∠BAD=∠BAA1=60°,求∠DAA1的大小.