题目内容
7.已知f(x)=$\left\{\begin{array}{l}{{2}^{|x-1|}-1,x≤2}\\{\frac{1}{2}f(x-2),x>2}\end{array}\right.$,g(x)=logax(a>1),若F(x)=f(x)-g(x)恰有三个不同零点,则实数a的取值范围为(4,${e}^{\frac{1}{ln2}}$)∪[16,256].( 参考值:ln2≈0.7 )分析 由x≤2时的f(x)解析式,可得当2<x≤4,当4<x≤6的解析式,由题意可得y=f(x)和y=g(x)的图象有三个交点.画出y=f(x)和y=g(x)的图象,通过图象观察即可得到所求范围.
解答  解:当x≤2时,f(x)=2|x-1|-1;
解:当x≤2时,f(x)=2|x-1|-1;
当2<x≤4,即0<x-2≤2时,f(x)=$\frac{1}{2}$f(x-2)
=$\frac{1}{2}$(2|x-3|-1);
当4<x≤6,即2<x-2≤4时,f(x)=$\frac{1}{2}$f(x-2)
=$\frac{1}{4}$(2|x-5|-1);
…,
F(x)=f(x)-g(x)恰有三个不同零点,
即为y=f(x)和y=g(x)的图象有三个交点.
画出y=f(x)和y=g(x)的图象,
当y=g(x)的图象通过点(4,$\frac{1}{2}$)时,
由loga4=$\frac{1}{2}$,解得a=16,图象恰好有三个交点;
当y=g(x)的图象经过点(4,$\frac{1}{4}$)时,
由loga4=$\frac{1}{4}$,解得a=256,图象恰好有三个交点.
由图象观察,可得16≤a≤256时,y=f(x)和y=g(x)都有三个交点.
由a>4时,f(x)与g(x)在x=1处相切,可得g′(x)|x=1=$\frac{1}{lna}$=ln2,
解得a=${e}^{\frac{1}{ln2}}$.
当4<a<${e}^{\frac{1}{ln2}}$时,在(1,2)有交点,即x=1一个解,(1,2)内一个解,(2,3)内有一解,
由4<a<${e}^{\frac{1}{ln2}}$,且loga4>$\frac{1}{4}$,可得4<a<${e}^{\frac{1}{ln2}}$.
故答案为:(4,${e}^{\frac{1}{ln2}}$)∪[16,256].
点评 本题考查分段函数的图象及运用,考查函数的零点的判断,注意运用数形结合的思想方法,考查对数的运算性质,属于中档题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案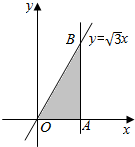 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x,y=0,x=t(t>0)围成的△OAB的面积为S(t),则S(t)在t=2时的瞬时变化率是2$\sqrt{3}$.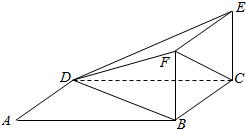 如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.
如图.ABCD为平行四边形,BCEF是边长为1的正方形.BF⊥BA,∠DAB=$\frac{π}{3}$,AB=2AD.