题目内容
求函数y=
cosx-
sinx在[0,π]上的最值和单调增区间.
| 6 |
| 2 |
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:化简函数的解析式为-2sin(x-
),通过x的范围,利用正弦函数的值域求出最值,利用正弦函数的单调减区间求出函数的增区间.
| π |
| 6 |
解答:
解:函数y=
cosx-
sinx=-2
sin(x-
),∵x∈[0,π],∴x-
∈[-
,
].
sin(x-
)∈[-
,1],∴y∈[-2
,
],
函数的最大值为
,最小值为-2
.
由2kπ+
≤x-
≤2kπ+π,k∈z,可得 2kπ+
≤x≤2kπ+
,k∈z,
k=0时,单调增区间为:[
,
].
函数在[0,π]上的单调增区间为:[
,π].
| 6 |
| 2 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
sin(x-
| π |
| 6 |
| 1 |
| 2 |
| 2 |
| 2 |
函数的最大值为
| 2 |
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
| 7π |
| 6 |
k=0时,单调增区间为:[
| 2π |
| 3 |
| 7π |
| 6 |
函数在[0,π]上的单调增区间为:[
| 2π |
| 3 |
点评:本题考查两角和的正弦公式,正弦函数的单调性,是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
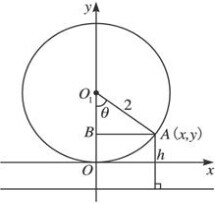 如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.
如图,某大风车的半径为2米,每12秒旋转一周,它的最低点O离地面0.5米.风车圆周上一点A从最低点O开始,运动t秒后与地面的距离为h米.以O为原点,过点O的圆的切线为x轴,建立直角坐标系.