题目内容
在等差数列{an}中,若a2=1,a8=2a6+a4,则a5的值是( )
| A、-5 | ||
B、-
| ||
C、
| ||
D、
|
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:设等差数列{an}的公差为d,由题意可得a1和d的方程组,解方程组代入等差数列的通项公式可求.
解答:
解:设等差数列{an}的公差为d,
∵a2=1,a8=2a6+a4,
∴a1+d=1,a1+7d=2(a1+5d)+a1+3d
联立解得a1=
,d=-
,
∴a5=a1+4d=
+4(-
)=-
故选:B
∵a2=1,a8=2a6+a4,
∴a1+d=1,a1+7d=2(a1+5d)+a1+3d
联立解得a1=
| 3 |
| 2 |
| 1 |
| 2 |
∴a5=a1+4d=
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:B
点评:本题考查等差数列的通项公式,求出数列的首项和公差是解决问题的关键,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正项等比数列{an}中,若log2(a1a9)=4,则a3a7等于( )
| A、16 | B、-16 |
| C、10 | D、256 |
已知函数f(x)(x∈R)满足f′(x)>f(x),则( )
| A、f(1)>ef(0)>e2f(-1) |
| B、f(1)<ef(0)<e2f(-1) |
| C、e2f(-1)>ef(0)>f(1) |
| D、e2f(-1)<ef(0)<f(1) |
已知命题p:若a,b是任意实数,且a>b,则a2>b2,
命题q:若a,b是任意实数,且a>b,则(
)a<(
)b.
在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,
真命题的个数是( )
命题q:若a,b是任意实数,且a>b,则(
| 1 |
| 2 |
| 1 |
| 2 |
在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,
真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
一个几何体的三视图如图所示,则该几何体的体积为( )
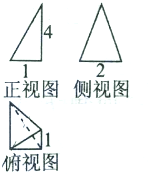

| A、2 | ||||
B、
| ||||
C、
|
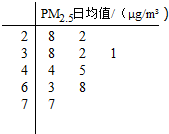 我国政府对PM2.5采用如下标准:
我国政府对PM2.5采用如下标准: