题目内容
8.在正三棱柱ABC-A1B1C1中,已知AB=2,D是棱BB1的中点,且BD=1,则C1与平面ADC的距离为( )| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
分析 以C为原点,在平面ABC为赤C作CB的垂线为x轴,以CB为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出C1与平面ADC的距离.
解答 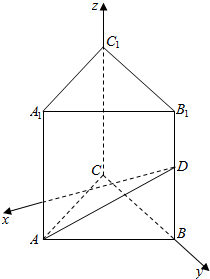 解:以C为原点,在平面ABC为赤C作CB的垂线为x轴,以CB为y轴,CC1为z轴,建立空间直角坐标系,
解:以C为原点,在平面ABC为赤C作CB的垂线为x轴,以CB为y轴,CC1为z轴,建立空间直角坐标系,
∵正三棱柱ABC-A1B1C1中,AB=2,D是棱BB1的中点,且BD=1,
∴C1(0,0,2),A($\sqrt{3}$,1,0),D(0,2,1),C(0,0,0),
$\overrightarrow{C{C}_{1}}$=(0,0,2),$\overrightarrow{CA}$=($\sqrt{3}$,1,0),$\overrightarrow{CD}$=(0,2,1),
设平面ADC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CA}=\sqrt{3}x+y=0}\\{\overrightarrow{n}•\overrightarrow{CD}=2y+z=0}\end{array}\right.$,取x=2,得$\overrightarrow{n}$=(2,-2$\sqrt{3}$,4$\sqrt{3}$),
∴C1与平面ADC的距离:d=$\frac{|\overrightarrow{C{C}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{|8\sqrt{3}|}{\sqrt{4+12+48}}$=$\sqrt{3}$.
故选:A.
点评 本题考查点到平面的距离的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

 阅读快车系列答案
阅读快车系列答案
 B.
B.  C.
C.  D.
D.
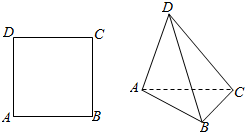 把边长为2的正方形ABCD沿对角线AC折成直二面角.求:
把边长为2的正方形ABCD沿对角线AC折成直二面角.求: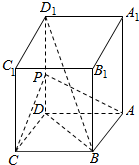 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.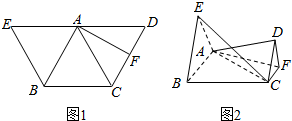 如图1,已知正三角形ABC,以AB、AC为边在同一平面内向外作正三角形ABE与ACD,F为CD中点,分别沿AB、AF将平面ABE、平面ADE折成直二面角,连接EC、CD,如图2所示.
如图1,已知正三角形ABC,以AB、AC为边在同一平面内向外作正三角形ABE与ACD,F为CD中点,分别沿AB、AF将平面ABE、平面ADE折成直二面角,连接EC、CD,如图2所示.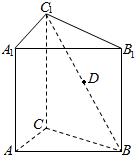 如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D为C1B的中点,P为AB边上的动点.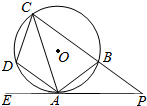 如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.
如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.