题目内容
19.已知-$\frac{π}{2}$<x<0,sinx+cosx=$\frac{1}{5}$.(1)求sin2x和cosx-sinx;
(2)求$\frac{sin2x+2si{n}^{2}x}{1-tanx}$的值.
分析 (1)由角在第四象限,得sinx<0,cosx>0,由(sinx+cosx)2=1+2sinxcosx=$\frac{1}{25}$,能求出sin2x和cosx-sinx.
(2)由sinx+cosx=$\frac{1}{5}$,cosx-sinx=$\frac{7}{5}$,先求出sinx=-$\frac{3}{5}$,cosx=$\frac{4}{5}$,由此能求出$\frac{sin2x+2si{n}^{2}x}{1-tanx}$的值.
解答 解:(1)∵-$\frac{π}{2}$<x<0,sinx+cosx=$\frac{1}{5}$,
∴sinx<0,cosx>0,
(sinx+cosx)2=1+2sinxcosx=$\frac{1}{25}$,
∴sin2x=2sinxcosx=-$\frac{24}{25}$,
(cosx-sinx)2=1-2cosxsinx=1+$\frac{24}{25}$=$\frac{49}{25}$,
∴cosx-sinx=$\frac{7}{5}$.
(2)由(1)得sinx+cosx=$\frac{1}{5}$,cosx-sinx=$\frac{7}{5}$,
∴sinx=-$\frac{3}{5}$,cosx=$\frac{4}{5}$,∴tanx=$\frac{sinx}{cosx}$=-$\frac{3}{4}$,
∴$\frac{sin2x+2si{n}^{2}x}{1-tanx}$=$\frac{-\frac{24}{25}+2×(-\frac{3}{5})^{2}}{1-(-\frac{3}{4})}$=-$\frac{24}{175}$.
点评 本题考查三角函数值的求法,是基础题,解题时要认真审题,注意同角三角函数关系式的合理运用.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案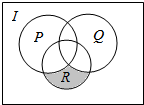 已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )
已知全集为I,集合P,Q,R如图所示,则图中阴影部分可以表示为( )| A. | R∩∁I(P∪Q) | B. | R∩∁I(P∩Q) | C. | (R∩∁IP)∩Q | D. | (R∩∁IQ)∩P |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
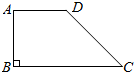 如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全部总人数的百分比为x,成绩大于等于15秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…;第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全部总人数的百分比为x,成绩大于等于15秒的学生人数为y,则从频率分布直方图中可分析出x和y分别为( )