题目内容
11．如图，直线a∥α，a?β，α∩β=b，求证：a∥b．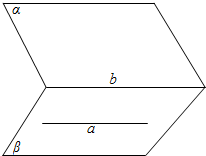
分析 由α∩β=b，得b?α，b?β，再由直线a∥α，利用线面平行的性质定理能证明a∥b．
解答 证明：∵α∩β=b，∴b?α，b?β，
∵直线a∥α，∴a与b没有交点，
∵a?β，b?β，
∴a∥b．
点评 本题考查线线平行的证明，是基础题，用线面平行的性质定理可以判定两直线是否平行，同时也提供了一种作平行线的方法．
练习册系列答案
相关题目
6．cosα（cosα-cosβ）+sinα（sinα-sinβ）的化简结果是（ ）
| A． | cos（α+β） | B． | cos（α-β） | C． | 2sin2$\frac{α-β}{2}$ | D． | 2sin2$\frac{α+β}{2}$ |
16．下列函数中是奇函数的为（ ）
| A． | y=$\frac{{x}^{2}+cosx}{{x}^{2}-cosx}$ | B． | y=$\frac{sinx+cosx}{sinx-cosx}$ | ||
| C． | y=2cosx | D． | y=lg（sinx+$\sqrt{1+si{n}^{2}x}$） |
15．下列函数中，既不是奇函数，也不是偶函数的是（ ）
| A． | $y=\sqrt{{x^2}+2}$ | B． | y=x+ex | C． | $y={3^x}+\frac{1}{3^x}$ | D． | $y=x-\frac{1}{x}$ |