题目内容
8.在直角坐标系xOy中,曲线${C_1}:\left\{\begin{array}{l}x=1+2t\\ y=2-2t\end{array}\right.$(t为参数,t∈R),曲线${C_2}:\left\{\begin{array}{l}x=2cosθ+2\\ y=2sinθ\end{array}\right.$(θ为参数,θ∈[0,2π]).(Ⅰ)以O为极点,x轴正半轴为极轴,取相同的长度单位建立极坐标系,求曲线C2的极坐标方程;
(Ⅱ)若曲线C1与曲线C2相交于点A、B,求|AB|.
分析 (Ⅰ)消去参数后得到其普通方程,把x=ρcosθ,y=ρsinθ代入可得曲线C2的极坐标方程;
(Ⅱ)法一:利用弦长公式直接求解,利用参数的几何意义求解.法二、运用直线的参数方程求解.
解答 解(Ⅰ)由$\left\{{\begin{array}{l}{x=2cosθ+2}\\{y=2sinθ}\end{array}}\right.$消去参数后得到其普通方程为x2-4x+y2=0,
把x=ρcosθ,y=ρsinθ代入可得ρ=4cosθ.
∴曲线C2的极坐标方程为ρ=4cosθ.
(Ⅱ)由$\left\{{\begin{array}{l}{x=1+2t}\\{y=2-2t}\end{array}}\right.$消去参数后得到其普通方程为x+y-3=0,
由曲线C2可知:以(2,0)为圆心,以2为半径的圆.
那么:圆心到直线C1的距离为$\frac{{|{1×2+1×0-3}|}}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$,
∴弦长$|{AB}|=2\sqrt{{2^2}-{{({\frac{{\sqrt{2}}}{2}})}^2}}=2×\frac{{\sqrt{14}}}{2}=\sqrt{14}$.
解法2:把${C_1}:\left\{{\begin{array}{l}{x=1+2t}\\{y=2-2t}\end{array}}\right.$代入x2-4x+y2=0得8t2-12t+1=0,
则有:${t_1}+{t_2}=\frac{3}{2}$,${t_1}{t_2}=\frac{1}{8}$,
则${|{{t_1}-t}|_2}=\sqrt{{{({{t_1}+{t_2}})}^2}-4{t_1}{t_2}}=\sqrt{{{({\frac{3}{2}})}^2}-4×\frac{1}{8}}=\frac{{\sqrt{7}}}{2}$,
根据直线方程的参数几何意义知$|{AB}|=2\sqrt{2}{|{{t_1}-t}|_2}=\sqrt{14}$.
点评 本题考查了直角坐标方程与极坐标、参数方程之间的转换,考查了参数方程的几何意义.属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 1008 | B. | 1010 | C. | 2016 | D. | 2017 |
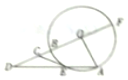 如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.
如图,圆O的半径OA与OB相互垂直,E为圆O上一点,直线OB与圆O交于另一点F,与直线AE交于点D,过点E的切线CE交线段于点C,求证:CD2=CB•CF.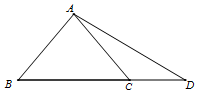 如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.
如图,△ABC是等腰直角三角形,∠bac=90°,点D在边BC的延长线上,且BC=2CD,$AD=\sqrt{5}$.