题目内容
18.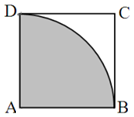 已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.
已知正方形ABCD的边长为1,弧BD是以点A为圆心的圆弧.(1)在正方形内任取一点M,求事件“|AM|≤1”的概率;
(2)用大豆将正方形均匀铺满,经清点,发现大豆一共28粒,其中有22粒落在圆中阴影部分内,请据此估计圆周率π的近似值(精确到0.01).
分析 (1)根据已知条件,求出满足条件的正方形ABCD的面积,及事件“|AM|≤1”对应平面区域的面积,代入几何概型计算公式,即可求出答案.
(2)正方形内的56粒芝麻颗粒中有44粒落在扇形BAD内,频率为$\frac{22}{28}$,用频率估计概率,由(1)知$\frac{π}{4}$,可得圆周率π的近似值.
解答  解:(1)如图,在边长为1的正方形ABCD内任取一点M,满足条件的点M落在扇形BAD内(图中阴影部分),由几何概型概率计算公式,有:$P({|{MA}|≤1})=\frac{{{S_{阴影部分}}}}{{{S_{正方形ABCD}}}}=\frac{π}{4}$,
解:(1)如图,在边长为1的正方形ABCD内任取一点M,满足条件的点M落在扇形BAD内(图中阴影部分),由几何概型概率计算公式,有:$P({|{MA}|≤1})=\frac{{{S_{阴影部分}}}}{{{S_{正方形ABCD}}}}=\frac{π}{4}$,
故事件“|AM|≤1”发生的概率为$\frac{π}{4}$.
(2)正方形内的28粒大豆有22粒落在扇形BAD内,
频率为$\frac{22}{28}=\frac{11}{14}$,
用频率估计概率,由(1)知$\frac{π}{4}≈\frac{11}{14}$,
∴$π≈\frac{11}{14}×4=\frac{22}{7}≈3.14$,即π的近似值为3.14.
点评 本题考查了随机模拟法求圆周率的问题,也考查了几何概率的应用问题,几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知命题p:?x<0,x2>0,那么¬P是( )
| A. | ?x≥0,x2≤0 | B. | ?x≥0,x2≤0 | C. | ?x<0,x2≤0 | D. | ?x<0,x2≤0 |
9.已知集合P={x|1<x<3},Q={x|x>2},则P∩Q=( )
| A. | (1,3) | B. | (2,3) | C. | (1,2) | D. | (2,+∞) |
13.圆(x-3)2+(y-3)2=4上到直线3x+4y-16=0的距离等于1的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.在△ABC中,a=3,b=4,sinA=$\frac{1}{3}$,则sinB=( )
| A. | $\frac{1}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{1}{12}$ | D. | $\frac{4}{9}$ |
7.已知单位向量$\overrightarrow a$和$\overrightarrow b$满足$|{\overrightarrow a-\overrightarrow b}|=\sqrt{3}|{\overrightarrow a+\overrightarrow b}|$,则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |