题目内容
用二分法求f(x)=x3+x2-2x-2在x的正半轴上的一个零点(误差不超过0.1).
[解析] 显然f(2)=23+22-2×2-2=6>0.
当x>2时f(x)>0,又f(0)=-2<0,f(1)=-2<0,
故f(x)在(1,2)区间内有零点.
| 区间 | 中点值 | 中点函数值 |
| [1,2] | 1.5 | 0.625 |
| [1,1.5] | 1.25 | -0.984 |
| [1.25,1.5] | 1.375 | -0.260 |
| [1.375,1.5] | 1.438 | 0.165 |
| [1.375,1.438] |
|

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
在一次数学试验中,应用图形计算器采集到如下一组数据:
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+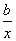
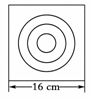 如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,
如图所示,在墙上挂着一块边长为16 cm的正方形木块,上面画了小、中、大三个同心圆,半径分别为2 cm,4 cm,6 cm,某人站在3 m之外向此板投镖,设镖击中线上或没有投中木板时不算,可重投,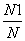 ,
,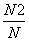 ,
,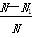 B.
B.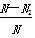
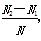 ,
,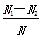
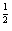 ,g(x)=(x
,g(x)=(x ,g(x)=x-3
,g(x)=x-3 是(-∞,+∞)上的增函数,那么a的取值范围是( )
是(-∞,+∞)上的增函数,那么a的取值范围是( ) ,3) D.(1,3)
,3) D.(1,3)