题目内容
7.已知正项等比数列{an}的公比q>1,且满足a2=6,a1a3+2a2a4+a3a5=900,设数列{an}的前n项和为Sn,若不等式λan≤1+Sn对一切n∈N*恒成立,则实数λ的最大值为$\frac{4}{3}$.分析 求出数列的公比,求出前n项和,利用不等式求解最值即可.
解答 解:正项等比数列{an}的前n项和为Sn,且a2=6,a1a3+2a2a4+a3a5=900,
可得a22+2a22q2+a22q4=900,
∴1+2q2+q4=25
解得q=2,
∴a1=3
∴an=a1qn-1=3×2n-1,
Sn=$\frac{3(1-{2}^{n})}{1-2}$=3×2n-3,
不等式λan≤1+Sn对一切n∈N*恒成立,
∴λ≤$\frac{1+{S}_{n}}{{a}_{n}}$=$\frac{3×{2}^{n}-2}{3×{2}^{n-1}}$,
∵2-$\frac{2}{3×{2}^{n-1}}$≥2-$\frac{2}{3}$=$\frac{4}{3}$,
则实数λ的最大值为:$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查数列的应用,数列求和,以及不等式的应用,最值的求法.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
18.已知函数$f(x)=\left\{\begin{array}{l}2-{log_2}(-x+2),0≤x<2\\ 2-f(-x),-2<x<0\end{array}\right.$则|f(x)|≤2的解集为( )
| A. | [0,1] | B. | (-2,1] | C. | $[-\frac{7}{4},2)$ | D. | $[{-\frac{7}{4},1}]$ |
2.已知复数z满足(1+i)•z=2-i(其中i为虚数单位),则|z|=( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\sqrt{10}$ |
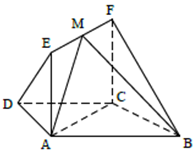 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,$CF=\sqrt{2}$.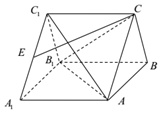 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E为A1C1的中点,$\frac{{C{C_1}}}{{{C_1}E}}=\sqrt{2}$