��Ŀ����
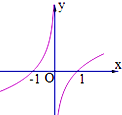
16����ֱ������ϵxOy�У�����C1�IJ���������$\left\{\begin{array}{l}{x=t-\frac{1}{t}}\\{y=t+\frac{1}{t}}\end{array}\right.$��tΪ��������������ԭ��Ϊ���㣬x���������Ϊ���Ὠ��������ϵ������C2�ļ����귽���Ǧ�sin����+$\frac{��}{3}$��=1����1��������C1����ͨ����������C2��ֱ�����귽�̣�
��2���������߽����ľ��룮
���� ��1����C1�IJ�����������ƽ���������ȥ����t�õ���ͨ���̣���C2�ļ����귽��չ�������ݼ�������ֱ������Ķ�Ӧ��ϵ�ó�C2��ֱ�����귽�̣�
��2�����C2�IJ������̣�����C1����ͨ���̣����ݲ����ļ�������ó������ľ��룮
��� �⣺��1��������C1�IJ���������$\left\{\begin{array}{l}{x=t-\frac{1}{t}}\\{y=t+\frac{1}{t}}\end{array}\right.$��tΪ��������
��$\left\{\begin{array}{l}{{x}^{2}={t}^{2}+\frac{1}{{t}^{2}}-2}\\{{y}^{2}={t}^{2}+\frac{1}{{t}^{2}}+2}\end{array}\right.$��
������C1����ͨ����Ϊy2-x2=4����$\frac{{y}^{2}}{4}-\frac{{x}^{2}}{4}=1$��
������C2�ļ����귽���Ǧ�sin����+$\frac{��}{3}$��=1����$\frac{1}{2}��sin��$+$\frac{\sqrt{3}}{2}$��cos��=1��
������C2��ֱ�����귽��Ϊ$\frac{1}{2}$y+$\frac{\sqrt{3}}{2}x$-1=0����$\sqrt{3}$x+y-2=0��
��2������C2��б��k=-$\sqrt{3}$���ҹ��㣨$\sqrt{3}$��-1����
��ֱ��C2�IJ�������Ϊ$\left\{\begin{array}{l}{x=\sqrt{3}-\frac{1}{2}t}\\{y=-1+\frac{\sqrt{3}}{2}t}\end{array}\right.$��tΪ��������
����C1����ͨ���̵ã�t2=12����t1=2$\sqrt{3}$��t2=-2$\sqrt{3}$��
�������߽����ľ���Ϊ|t1-t2|=4$\sqrt{3}$��
���� ���⿼���˲������̣������귽������ͨ���̵�ת���������ļ������弰Ӧ�ã����е��⣮

 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д� Сѧ��ѧ������ѿڶ���ϵ�д�
Сѧ��ѧ������ѿڶ���ϵ�д� ������Ӧ�������������ϵ�д�
������Ӧ�������������ϵ�д�| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | $-\frac{1}{2}$ | D�� | -2 |