题目内容
下列命题:①?x∈C,x2≥0;②?x∈R,x2≥x;③7≥7;④“x2≠1”的充要条件是“x≠1或x≠-1”,其中真命题的个数是( )
| A、0 | B、1 | C、2 | D、3 |
考点:全称命题,特称命题
专题:简易逻辑
分析:分别根据含有量词的命题的性质进行判断即可得到结论.
解答:
解:①?x∈C,x2≥0;错误,当x=i时,i2=-1≤0,不成立.故①错误;
②当x=0时,x2≥x成立,故②正确;
③7≥7成立;故③正确;
④“x2≠1”的充要条件是“x≠1且x≠-1”,故④错误,
故选:C
②当x=0时,x2≥x成立,故②正确;
③7≥7成立;故③正确;
④“x2≠1”的充要条件是“x≠1且x≠-1”,故④错误,
故选:C
点评:本题主要考查命题的真假判断,根据含有量词的命题的性质以及充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
相关题目
球的半径是5,则它的体积是( )
| A、400π | ||
| B、100π | ||
C、
| ||
D、
|
一个三角形的三边长依次是4、6、2
,这个三角形的面积等于( )
| 7 |
A、3
| ||
B、6
| ||
C、3
| ||
D、6
|
如图,已知△ABC中,D为BC边上的中点,则下列等式中正确的是( )
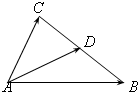

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
如图,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=( )
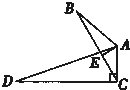

| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2
,则b等于( )
| 3 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
已知O为极点,曲线C1,C2都在极轴的上方,极坐标方程为C1:ρ=2cosθ(0≤θ≤π),C2:ρ=2(0≤θ≤π).若直线θ=α(ρ∈R,0≤α<π)与曲线C1,C2交于M,N(M不同于点O)两点,则OM2+MN2的最小值为( )
| A、1 | B、2 | C、3 | D、4 |
设f(x)是一次函数,f(8)=15,f(2),f(5),f(14)成等比数列,令Sn=f(1)+f(2)+f(3)+…+f(n),则Sn等于( )
| A、n2 |
| B、n2-n |
| C、n2+n |
| D、以上都不对 |