题目内容
在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若
=
，那么△ABC一定是（ ）
| b2 |
| a2 |
| tanB |
| tanA |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、直角三角形或等腰三角形 |
考点：正弦定理
专题：解三角形
分析：直接利用正弦定理化简等式，推出A、B关系，即可判断三角形的形状．
解答：
解：
=
，由正弦定理可得：
=
，
sinAcosA=sinBcosB，
可得sin2A=sin2B，∴2A=2B或2A+2B=π，
即A=B或A+B=
，
所以三角形是直角三角形或等腰三角形．
故选：D．
| b2 |
| a2 |
| tanB |
| tanA |
| sin2B |
| sin2A |
| sinBcosA |
| sinAcosB |
sinAcosA=sinBcosB，
可得sin2A=sin2B，∴2A=2B或2A+2B=π，
即A=B或A+B=
| π |
| 2 |
所以三角形是直角三角形或等腰三角形．
故选：D．
点评：本题考查三角形形状的判断，正弦定理的应用，考查计算能力．
练习册系列答案
相关题目
四位同学研究了函数y=x+
的有关性质，得到以下四个结论，其中正确的是（ ）
①该函数既没有最大值也没有最小值；
②该函数既有极大值也有极小值；
③该函数的极大值小于极小值；
④该函数的最大值大于最小值．
| 1 |
| x |
①该函数既没有最大值也没有最小值；
②该函数既有极大值也有极小值；
③该函数的极大值小于极小值；
④该函数的最大值大于最小值．
| A、②④ | B、①③ | C、①② | D、①②③ |
若|
|=2，|
|=
，
与
的夹角为45°，要使k
-
与
垂直，则k=（ ）
| a |
| b |
| 2 |
| a |
| b |
| b |
| a |
| a |
| A、±2 | ||
B、±
| ||
C、
| ||
| D、2 |
复数Z=1+（2-sinθ）i在复平面内对应的点所在象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设Z=
+（a2+2a-15）i为实数时，实数a的值是（ ）
| a-5 |
| a2+4a-5 |
| A、3 | B、-5 |
| C、3或-5 | D、-3或5 |
如图，∠B=∠D，AE⊥BC，∠ACD=90°，且AB=6，AC=4，AD=12，则BE=（ ）
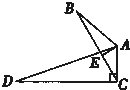
| A、3 | ||
| B、4 | ||
C、4
| ||
| D、5 |
下列命题错误的是（ ）
| A、命题“若m＞0，则方程x2+x-m=0有实数根”的逆否命题为：“若方程x2+x-m=0无实数根，则m≤0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若p且q为假命题，则p，q均为假命题 |
| D、空间中，没有公共点的两直线不一定平行 |
设动点P（x，y）满足：
=|x+y-2|，则点P的轨迹为（ ）
| 2x2+2(y-2)2 |
| A、直线 | B、抛物线 |
| C、椭圆 | D、双曲线 |