Question

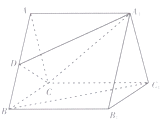
【题目】已知二面角 为 为垂足， ,则异面直线 与 所成角的余弦值为（ ）
A.
B.
C.
D.

Answer 1

【答案】B
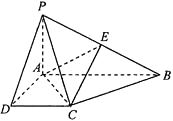
【解析】如图所示，过点 作 ，使 ，垂足为 ，过点 作 ，过点 作 ，连接 ，因为 ，所以 ，因为 ，又 ，所以 ，所以 ，在 中，设 ，则 ，在 中，则 ，在 中，则 ，所以异面直线 与 所成的角，即是 ,所以 ，所以答案是：B．

【考点精析】本题主要考查了异面直线及其所成的角和空间向量的数量积运算的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；等于的长度与在的方向上的投影的乘积才能正确解答此题．