Question

【题目】如图，在三棱柱 中，底面 是边长为2的等边三角形， 为 的中点.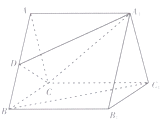

（1）求证： 平面 ；
（2）若四边形 是正方形，且 ， 求直线 与平面 所成角的正弦值.

Answer 1

【答案】
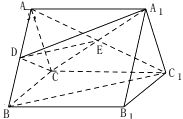
（1）证明：连接AC1，设AC1与A1C交于点E ，连接 ，则 为 中点，

为 的中点,

∴ 平面 .

（2）解：取 的中点 ，连结 ，则

，故 ，∴

, 平面

取 中点 ，连结 ，过点作 ，则MN平面BCC1B1

连结 ， ，

为直线 与平面 所成的角，

即直线 与平面所 成的角的正弦值为 .

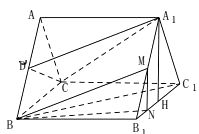
【解析】（1）连接AC1交A1C于点E，连接DE，则DE为三角形ABC1的中位线，根据线面平行的判定定理即可证明；（2）取B1C1 的中点 H ，连结 A1H ，则根据线面垂直的判定定理易知A1H平面BCC1B1，取A1B1的中点M，过点M作MNA1H，则MN平面BCC1B1，因为A1DBM，所以即为直线A1D与平面BCC1B1所成角.
【考点精析】认真审题，首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行)，还要掌握空间角的异面直线所成的角(已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则)的相关知识才是答题的关键．