题目内容
9.已知点O为△ABC的外心,且AC=4,AB=2,则$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=6.分析 根据向量射影定理,数量积的运算性质即可得出.
解答 解:O为△ABC的外心,且AC=4,AB=2,
∴$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AO}$$•\overrightarrow{AC}$-$\overrightarrow{AO}$•$\overrightarrow{AB}$=|$\overrightarrow{AO}$|•|$\overrightarrow{AC}$|cos120°-|$\overrightarrow{AO}$|•|$\overrightarrow{AB}$|cos120°=$\frac{1}{2}$|$\overrightarrow{AC}$|2-$\frac{1}{2}$|$\overrightarrow{AB}$|2=$\frac{1}{2}$×16-$\frac{1}{2}$×4=6,
故答案为:6.
点评 本题主要考查向量数量积的几何意义.要会巧妙的转化问题.属中档题.

练习册系列答案
相关题目
20.在△ABC中,已知a=1,b=$\sqrt{3}$,A=120°,则此三角形( )
| A. | 无解 | B. | 有一解 | C. | 有两解 | D. | 解的个数不确定 |
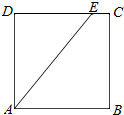 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.