题目内容
1．下列说法正确的是（ ）| A． | 若p∧q为假命题，则p、q均为假命题 | |
| B． | 命题“若x2=1，则x=1”为真命题 | |
| C． | 命题“若x=y，则sinx=siny”的逆否命题为真命题 | |
| D． | 命题“存在一个实数x，使不等式x2-3x+6＜0成立”为真命题 |
分析 A，p、q中只要有一个为假命题，p∧q为假命题；
B，若x2=1，则x=±1，故错；
C，判定原命题为真命题，其逆否命题与原命题同真假即可；
D，不等式x2-3x+6＜0无解．
解答 解：对于A，p、q中只要有一个为假命题，p∧q为假命题，故错；
对于B，若x2=1，则x=±1，故错；
对于C，原命题“若x=y，则sinx=siny”为真命题，其逆否命题与原命题同真假，故为真命题，故正确；
对于D，不等式x2-3x+6＜0无解，故错．
故选：C．
点评 本题考查了命题的真假判定，属于基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
11．记不等式组$\left\{\begin{array}{l}4x+3y≥10\\ x≤5\\ y≤4\end{array}\right.$表示的平面区域为D，过区域D中任意一点P作圆x2+y2=1的两条切线，切点分别为A，B，则当∠APB的最大时，cos∠APB为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
12．已知$x，y∈[-\frac{π}{4}，\frac{π}{4}]，a∈R$，且x3+sinx-2a=0，4y3+$\frac{1}{2}$sin2y+a=0，则cos（x+2y）的值为（ ）
| A． | 0 | B． | $\frac{1}{4}$ | C． | $-\frac{1}{2}$ | D． | 1 |
10．已知关于x的不等式x2-4ax+3a2＜0（a＞0）的解集为（x1，x2），则${x_1}+{x_2}+\frac{a}{{{x_1}{x_2}}}$的最小值是（ ）
| A． | $\frac{{\sqrt{6}}}{3}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{4\sqrt{3}}}{3}$ | D． | $-\frac{{4\sqrt{3}}}{3}$ |
17．
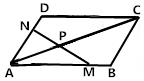如图，在?ABCD中，M，N分别为AB，AD上的点，且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$，$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$，连接AC，MN交于P点，若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$，则λ的值为（ ）
如图，在?ABCD中，M，N分别为AB，AD上的点，且$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$，$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$，连接AC，MN交于P点，若$\overrightarrow{AP}$=λ$\overrightarrow{AC}$，则λ的值为（ ）| A． | $\frac{3}{5}$ | B． | $\frac{3}{7}$ | C． | $\frac{6}{13}$ | D． | $\frac{6}{17}$ |