题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)若离心率为
| ||
| 3 |
(2)若椭圆上存在点P,使得∠APB=90°,求椭圆离心率e的取值范围;
(3)设直线AB与x轴、y轴分别交于点M,N,求证:
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意知
,由此能求出椭圆方程.
(2)由已知条件得四边形OBPA是边长为b=2的正方形,从而|OP|=2
=
b,|OP|2=8=2b2≤9=a2,a2≤2c2,由此能求出椭圆离心率e的取值范围.
(3)设P(x0,y0),A(x1,y1),B(x2,y2),则PA方程为:x1x+y1y=4,PB方程为:x2x+y2y=4.直线AB方程为x0x+y0y=4.从而|ON|=|y|=
,|OM|=|x|=
,由此能证明
+
为定值
.
|
(2)由已知条件得四边形OBPA是边长为b=2的正方形,从而|OP|=2
| 2 |
| 2 |
(3)设P(x0,y0),A(x1,y1),B(x2,y2),则PA方程为:x1x+y1y=4,PB方程为:x2x+y2y=4.直线AB方程为x0x+y0y=4.从而|ON|=|y|=
| 4 |
| |y0| |
| 4 |
| |x0| |
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
| 9 |
| 4 |
解答:
(1)解:∵椭圆C:
+
=1(a>b>0)离心率为
,
短轴一个端点到右焦点距离为3,
∴
,解得a=3,c=
,b=2,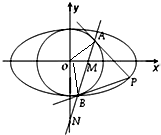
∴椭圆方程为
+
=1.
(2)解:∵过椭圆上一点P引圆O的两条切线,切点分别为A,B.
∠APB=90°,
∴四边形OBPA是边长为b=2的正方形,
∴|OP|=2
=
b,
∴|OP|2=8=2b2≤9=a2,∴a2≤2c2,
∴e2≥
,∴椭圆离心率e的取值范围是:
≤e<1.
(3)证明:设P(x0,y0),A(x1,y1),B(x2,y2),
则
=-
,
整理得x0x+y0y=x12+y12,∵x12+y12=4,
∴PA方程为:x1x+y1y=4,PB方程为:x2x+y2y=4.
∴x1x+y1y=x2x+y2y,∴
=-
,
直线AB方程为y-y1=-
(x-x1),即x0x+y0y=4.
令x=0,得|ON|=|y|=
,令y=0,得|OM|=|x|=
,
∴
+
=
+
=
+
=
=
.
∴
+
为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
短轴一个端点到右焦点距离为3,
∴
|
| 5 |

∴椭圆方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)解:∵过椭圆上一点P引圆O的两条切线,切点分别为A,B.
∠APB=90°,
∴四边形OBPA是边长为b=2的正方形,
∴|OP|=2
| 2 |
| 2 |
∴|OP|2=8=2b2≤9=a2,∴a2≤2c2,
∴e2≥
| 1 |
| 2 |
| ||
| 2 |
(3)证明:设P(x0,y0),A(x1,y1),B(x2,y2),
则
| y0-y1 |
| x0-x1 |
| x1 |
| y1 |
整理得x0x+y0y=x12+y12,∵x12+y12=4,
∴PA方程为:x1x+y1y=4,PB方程为:x2x+y2y=4.
∴x1x+y1y=x2x+y2y,∴
| y2-y1 |
| x2-x1 |
| x0 |
| y0 |
直线AB方程为y-y1=-
| x0 |
| y0 |
令x=0,得|ON|=|y|=
| 4 |
| |y0| |
| 4 |
| |x0| |
∴
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
| 9 | ||
|
| 4 | ||
|
| 9y02 |
| 16 |
| 4x02 |
| 16 |
| 36 |
| 16 |
| 9 |
| 4 |
∴
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |
| 9 |
| 4 |
点评:本题考查椭圆方程的求法,考查椭圆离心率e的取值范围的求法,考查
+
为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.
| a2 |
| |ON|2 |
| b2 |
| |OM|2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| B、函数f(x)=x-sinx(x∈R)有三个零点 |
| C、若p∧q为真命题,则p,q均为真命题 |
| D、若命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,x2+x+1≥0 |
某种产品的广告费支出x(百万元)与销售额y(百万元)有如下对应关系:则销售额y(百万元)关于广告费支出x(百万元)的回归直线方程是( )
| x | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| y | 96 | 97 | 99 | 100 | 101 | 103 | 104 |
A、
| ||
B、
| ||
C、
| ||
D、
|

 如图,三棱柱ABC-A1B1C1的所有棱长都相等,且AA1⊥底面ABC,D为CC1的中点,AB1与A1B相交于点O,连结OD.
如图,三棱柱ABC-A1B1C1的所有棱长都相等,且AA1⊥底面ABC,D为CC1的中点,AB1与A1B相交于点O,连结OD. 如图,△ABCD中,E,F分别是BC,DC的中点,G为交点,若
如图,△ABCD中,E,F分别是BC,DC的中点,G为交点,若