题目内容
如图,已知圆A,圆B都经过点C,BC是圆A的切线,圆B交AB于点D,连接CD并延长、交圆A于点E,连接AE.求证:DE·DC=2AD·DB.
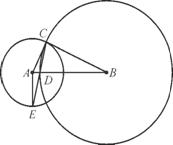
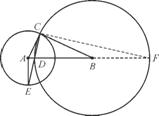
(第7题)
由已知,AC⊥BC,因为∠ACD+∠BCD=90°,
AC=AE,
BC=BD,
所以∠ACD=∠E,∠BCD=∠BDC.
又∠ADE=∠BDC,所以∠E+∠ADE=90°,
所以AE⊥AB.
延长DB交☉B于点F,连接FC,则DF=2DB,∠DCF=90°,
所以∠ACD=∠F,所以∠E=∠F,
所以RtADE∽RtCDF,
所以
=
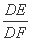,所以DE·DC=AD·DF.
又DF=2DB,所以DE·DC=2AD·DB.
练习册系列答案
相关题目
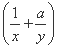≥9对任意正实数x,y恒成立,那么正实数a的最小值为 . 
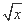)8的展开式中不含x4项的系数的和为 .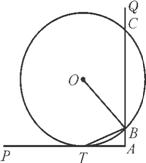
h(S+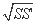
+S'),其中S',S分别为上、下底面面积,h为台体高)
A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
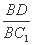的值.