题目内容
直三棱柱ABC-A1B1C1的所有顶点都在半径为
的球面上,且AB=AC=1,BC=
,求此三棱柱的体积.
| 5 |
| 2 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由于直三棱柱ABC-A1B1C1的底面ABC为直角三角形,我们可以把直三棱柱ABC-A1B1C1补成四棱柱,则四棱柱的体对角线是其外接球的直径,通过外接球的半径,求出该三棱柱的高.然后求解体积.
解答:
解:由题意,三棱柱ABC-A1B1C1为直三棱柱ABC-A1B1C1,底面ABC为直角三角形,把直三棱柱ABC-A1B1C1补成四棱柱,则四棱柱的体对角线是其外接球的直径,
所以棱锥的高为:2
=3
,
则三棱柱ABC-A1B1C1的体积为:
×1×1×3
=
.
故答案为:
.
所以棱锥的高为:2
(
|
| 2 |
则三棱柱ABC-A1B1C1的体积为:
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |
点评:本题考查球的球的内接体问题,关键是由组合体的位置关系得到球的半径的关系式,考查学生空间想象能力,是基础题.

练习册系列答案
相关题目
已知平面向量
,
,|
|=2,
=(2,
),若|
-
|=
,则
•
的值是( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=x3-3x+m恰有2个不同的零点,则实数m的值为( )
| A、±2 | B、±1 |
| C、-2或1 | D、-1或2 |
 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D. 
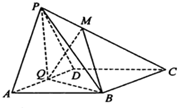 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.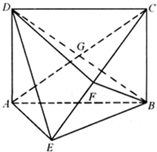 如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.
如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.