题目内容
16.若函数f(x)满足f(4)=2,且对于任意正数x1,x2,都有f(x1•x2)=f(x1)+f(x2)成立.则f(x)可能为( )| A. | $f(x)=\sqrt{x}$ | B. | $f(x)=\frac{x}{2}$ | C. | f(x)=log2x | D. | f(x)=2x |
分析 对A、B、C、D中的四种基本初等函数的运算性质逐一分析即可得到答案.
解答 解:对于A,∵$f(x)=\sqrt{x}$,∴f(x1•x2)=$\sqrt{{x}_{1}{•x}_{2}}$≠$\sqrt{{x}_{1}}$+$\sqrt{{x}_{2}}$,故A错误;
对于B,$f(x)=\frac{x}{2}$,同理可得f(x1•x2)≠f(x1)+f(x2),故B错误;
对于C,∵f(x)=log2x,∴f(x1•x2)=log2(x1•x2)=log2(x1)+log2(x2)=f(x1)+f(x2)成立.故C正确;
对于D,∵f(x)=2x,∴f(4)=24=16≠2,故D错误.
故选:C.
点评 本题考查抽象函数及其应用,突出考查基本初等函数的运算性质,属于中档题.

练习册系列答案
相关题目
7.已知函数f(x)=kx+1在区间(-1,1)上存在零点,则实数k的取值范围是( )
| A. | -1<k<1 | B. | k>1 | C. | k<-1 | D. | k<-1或k>1 |
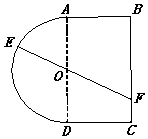 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.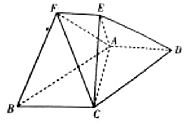 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.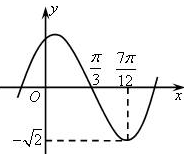 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).