题目内容
8.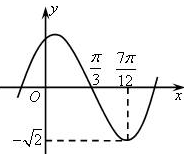 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
分析 根据三角函数的图象,求出函数的周期,进而求出ω和φ即可得到结论.
解答 解:由图象得A=$\sqrt{2}$,$\frac{T}{4}$=$\frac{7π}{12}$-$\frac{π}{3}$=$\frac{π}{4}$,
则周期T=π=$\frac{2π}{ω}$,
则ω=2,
则y=$\sqrt{2}$sin(2x+φ),
当x=$\frac{7π}{12}$时,y=-$\sqrt{2}$,
则$\sqrt{2}$sin(2×$\frac{7π}{12}$+φ)=-$\sqrt{2}$,
即sin($\frac{7}{6}$π+φ)=-1
即$\frac{7}{6}$π+φ=-$\frac{π}{2}$+2kπ,
即φ=-$\frac{5π}{3}$+2kπ,k∈Z,
∵|φ|<$\frac{π}{2}$,
∴当k=1时,φ=-$\frac{5π}{3}$+2π=$\frac{π}{3}$,
则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$),
故答案为:y=$\sqrt{2}$sin(2x+$\frac{π}{3}$)
点评 本题主要考查三角函数解析式的求解,根据三角函数图象求出A,ω 和φ的值是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
16.若函数f(x)满足f(4)=2,且对于任意正数x1,x2,都有f(x1•x2)=f(x1)+f(x2)成立.则f(x)可能为( )
| A. | $f(x)=\sqrt{x}$ | B. | $f(x)=\frac{x}{2}$ | C. | f(x)=log2x | D. | f(x)=2x |
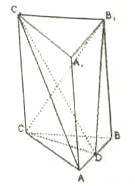 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.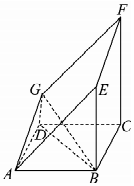 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.