题目内容
已知集合A={t|t2-4≤0}，对于满足集合A的所有实数t，使不等式x2+tx-t＞2x-1恒成立的x的取值范围为（ ）
| A、（-∞，1）∪（3，+∞） |
| B、（-∞，-1）∪（3，+∞） |
| C、（-∞，-1） |
| D、（3，+∞） |
考点：函数恒成立问题
专题：不等式的解法及应用
分析：由条件求出t的范围，不等式x2+tx-t＞2x-1变形为x2+tx-t-2x+1＞0恒成立，即不等式（x+t-1）（x-1）＞0恒成立，再由不等式的左边两个因式同为正或
同为负处理．
同为负处理．
解答：
解：由t2-4≤0得，-2≤t≤2，∴-1≤1-t≤3
不等式x2+tx-t＞2x-1恒成立，即不等式x2+tx-t-2x+1＞0恒成立，即不等式（x+t-1）（x-1）＞0恒成立，
∴只需
或
恒成立，
∴只需
或
恒成立，∵-1≤1-t≤3
只需x＞3或x＜-1即可．
故选：B．
不等式x2+tx-t＞2x-1恒成立，即不等式x2+tx-t-2x+1＞0恒成立，即不等式（x+t-1）（x-1）＞0恒成立，
∴只需
|
|
∴只需
|
|
只需x＞3或x＜-1即可．
故选：B．
点评：本题考查了一元二次不等式的解法问题，难度较大，充分利用恒成立的思想解题是关键．
练习册系列答案
阅读快车系列答案
相关题目
设集合A={-3，-2，-1，0，1}，集合B={x|x2-4=0}，则A∩B=（ ）
| A、{-2} | B、{2} |
| C、{-2，2} | D、∅ |
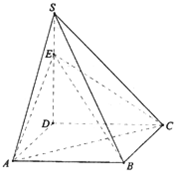如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．请利用空间向量解决下列问题：