题目内容
已知 ,其中e为自然对数的底数.
,其中e为自然对数的底数.
(I)若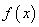 在
在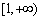 是增函数,求实数
是增函数,求实数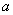 的取值范围;
的取值范围;
(II)当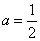 时,求函数
时,求函数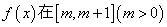 上的最小值;
上的最小值;
(III)求证: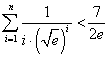 .
.
解:(Ⅰ)由题意知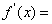
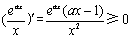 在
在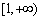 上恒成立.
上恒成立.
又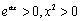 ,则
,则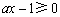 在
在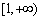 上恒成立,
上恒成立,
即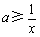 在
在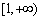 上恒成立. 而当
上恒成立. 而当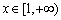 时,
时,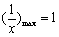 ,所以
,所以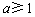 ,
,
于是实数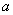 的取值范围是
的取值范围是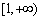 . ………………………………4分
. ………………………………4分
(Ⅱ)当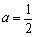 时,则
时,则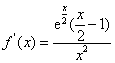 .
.
当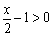 ,即
,即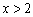 时,
时,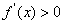 ;
;
当 ,即
,即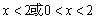 时,
时,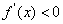 .
.
则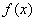 的增区间为(2,+∞),减区间为(-∞,0),(0,2). ……6分
的增区间为(2,+∞),减区间为(-∞,0),(0,2). ……6分
因为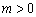 ,所以
,所以 ,
,
①当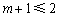 ,即
,即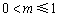 时,
时,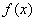 在[
在[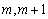 ]上单调递减,
]上单调递减,
所以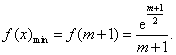
②当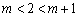 ,即
,即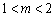 时,
时,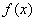 在
在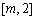 上单调递减,
上单调递减,
在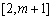 上单调递增,所以
上单调递增,所以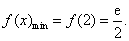
③当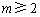 时,
时,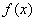 在[
在[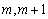 ]上单调递增,所以
]上单调递增,所以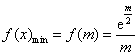 .
.
综上,当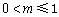 时,
时,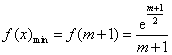 ;
;
当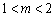 时,
时,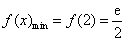 ;
;
当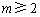 时,
时,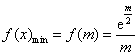 . …………………………9分
. …………………………9分
(Ⅲ)由(Ⅱ)可知,当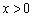 时,
时,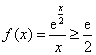 ,所以
,所以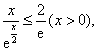
可得 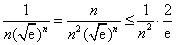 ………………………………11分
………………………………11分
于是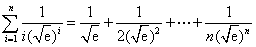
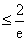
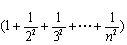
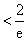
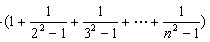
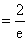
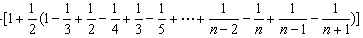
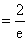
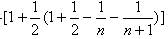
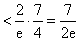 ……………………………………14分
……………………………………14分
【思路点拨】(Ⅰ)由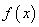 是增函数,转化为
是增函数,转化为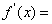
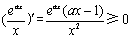 在
在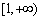 上恒成立. 即
上恒成立. 即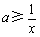 在
在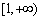 上恒成立. 最后得实数
上恒成立. 最后得实数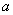 的取值范围(II)当
的取值范围(II)当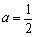 时,求出
时,求出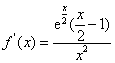 .利用
.利用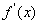 在求出单调区间,然后用分类讨论的思想方法解得
在求出单调区间,然后用分类讨论的思想方法解得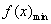
(III)由(Ⅱ)可知,当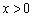 时,
时,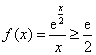 ,所以
,所以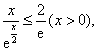
可得 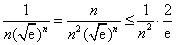 ,然后利用放缩法证明不等式即可.
,然后利用放缩法证明不等式即可.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
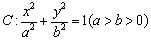 的左、右焦点分别为
的左、右焦点分别为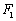 、
、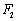 ,过
,过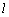 与椭圆
与椭圆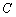 交于点
交于点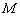 、
、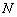 .
.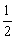 ,右准线的方程为
,右准线的方程为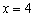 ,
,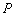 ,求
,求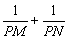 的
的 值;
值;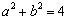 时,设
时,设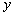 轴于点
轴于点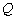 ,
,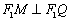 ,证明:点
,证明:点 B.
B. C.
C. D.
D.

 的部分图象如图所示.
的部分图象如图所示. 的内角分别是A,B,C,若
的内角分别是A,B,C,若 的值.
的值.
 的公差为
的公差为 ,
, ,前
,前 项和为
项和为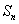 ,则
,则 的数值是 .
的数值是 .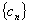 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列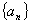 的前
的前 ,
, (
( ),则数列
),则数列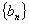 的变号数为 .
的变号数为 . ________.
________. ,过点F且斜率为k的直线与C交于A,B两点,若
,过点F且斜率为k的直线与C交于A,B两点,若 ,则k=
,则k= B.
B. C.
C.  D.
D.