题目内容
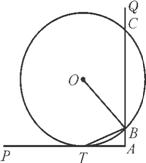
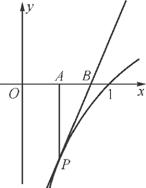
已知P(x0,y0)是函数f(x)=ln x图象上一点,在点P处的切线l与x轴交于点B,过点P作x轴的垂线,垂足为A.
(1) 求切线l的方程及点B的坐标;
(2) 若x0∈(0,1),求△PAB的面积S的最大值,并求此时x0的取值.(可能用到的公式: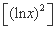 '=
'=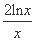 )
)
(1) 因为f'(x)= . ,
. ,
所以过点P的切线方程为y-ln x0=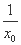 (x-x0),
(x-x0),
即切线方程为y=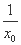 x+ln x0-1,
x+ln x0-1,
令y=0,得x=x0-x0ln x0,
即点B的坐标为(x0-x0ln x0,0).
(2) AB=x0-x0ln x0-x0=-x0ln x0,
PA=|f(x0)|=-ln x0,
所以S=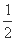 AB·PA=
AB·PA=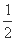 x0·(ln x0)2,
x0·(ln x0)2,
S'=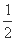 ln2 x0+
ln2 x0+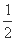 x0·2ln x0·
x0·2ln x0·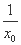
=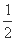 ln x0(ln x0+2),
ln x0(ln x0+2),
由S'>0,得0<x< ,所以当x∈
,所以当x∈ 时,S单调递增;由S'<0,得
时,S单调递增;由S'<0,得 <x<1,
<x<1,
所以当x∈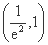 时,S单调递减.
时,S单调递减.
所以Smax=S =
= ln2
ln2 =
= .
.
所以当x0= ,面积S的最大值为
,面积S的最大值为 .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 sin(2x+
sin(2x+ )+6sinxcosx-2cos2x+1,x∈R.
)+6sinxcosx-2cos2x+1,x∈R. ]上的最大值和最小值.
]上的最大值和最小值.
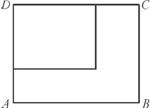
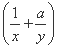 ≥9对任意正实数x,y恒成立,那么正实数a的最小值为 .
≥9对任意正实数x,y恒成立,那么正实数a的最小值为 .