题目内容
设F1、F2是双曲线x2-
=1的两个焦点,是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于 .
| y2 |
| 3 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题设条件,结合双曲线的性质,能求出|PF1|,|PF2|,|F1F2|的长,由此能求出△PF1F2的面积.
解答:
解:∵3|PF1|=4|PF2|,
∴设|PF1|=4k,|PF2|=3k,k>0,
∵P为双曲线x2-
=1上的一点,F1,F2是双曲线的两个焦点,
则由双曲线的定义,知:4k-3k=2,解得k=2,
∴|PF1|=8,|PF2|=6,
∵|F1F2|=4,
∴cos∠F1PF2=
=
,
∴sin∠F1PF2=
,
∴△PF1F2的面积等于
×8×6×
=3
.
故答案为:3
.
∴设|PF1|=4k,|PF2|=3k,k>0,
∵P为双曲线x2-
| y2 |
| 3 |
则由双曲线的定义,知:4k-3k=2,解得k=2,
∴|PF1|=8,|PF2|=6,
∵|F1F2|=4,
∴cos∠F1PF2=
| 64+36-16 |
| 2×8×6 |
| 7 |
| 8 |
∴sin∠F1PF2=
| ||
| 8 |
∴△PF1F2的面积等于
| 1 |
| 2 |
| ||
| 8 |
| 15 |
故答案为:3
| 15 |
点评:本题考查三角形的面积的求法,是中档题,解题时要熟练掌握双曲线的简单性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
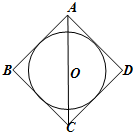 如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )A、2:
| ||
B、2
| ||
C、2:
| ||
D、
|
圆锥的母线长为2,侧面展开图是一个半圆,则此圆锥的表面积为( )
| A、6π | B、5π | C、3π | D、2π |