题目内容
设正项等比数列{an},已知a2=2,a3a4a5=29.
(1)求首项a1和公比q的值;
(2)若数列{bn}满足bn=
[lga1+lga2+…lgan-1+lg(kan)],问是否存在正数k,使数列{bn}为等差数列?若存在,求k的值.若不存在,说明理由.
(1)求首项a1和公比q的值;
(2)若数列{bn}满足bn=
| 1 |
| n |
考点:等差数列与等比数列的综合,等差关系的确定
专题:等差数列与等比数列
分析:(1)根据等比数列的性质,由a3a4a5=29求得到a4的值,然后利用a4比上a2求出q的值,再由a4的值和q的值即可求出首项a1的值;
(2)把等比数列的通项公式代入bn=
[lga1+lga2+…lgan-1+lg(kan)],利用对数的运算性质化简,由bn+1-bn为常数求得k的值.
(2)把等比数列的通项公式代入bn=
| 1 |
| n |
解答:
解:(1)∵a3a4a5=(a4)3=29,得a4=23=8(a4>0),
∴
=q2=4,q=2.
又由a4=a1q3,即8=a1•23,解得a1=1;
(2)证明:由(1)知,an=2n-1.
bn=
[lga1+lga2+…lgan-1+lg(kan)]
=
[lg(ka1a2…an)]=
[lg(k•20+1+2+…+(n-1))]=
[lgk+lg2
]=
+
lg2,
若数列{bn}为等差数列,则bn+1-bn=
+
lg2-
-
lg2
=lgk(
-
)+
lg2=-
lgk+
lg2为常数.
则lgk=0,k=1.
∴存在正数k=1,使数列{bn}为等差数列.
∴
| a4 |
| a2 |
又由a4=a1q3,即8=a1•23,解得a1=1;
(2)证明:由(1)知,an=2n-1.
bn=
| 1 |
| n |
=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
| n(n-1) |
| 2 |
| lgk |
| n |
| n-1 |
| 2 |
若数列{bn}为等差数列,则bn+1-bn=
| lgk |
| n+1 |
| n |
| 2 |
| lgk |
| n |
| n-1 |
| 2 |
=lgk(
| 1 |
| n+1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
则lgk=0,k=1.
∴存在正数k=1,使数列{bn}为等差数列.
点评:本题是等差数列和等比数列的综合题,考查了等比数列的性质,考查了等差数列的前n项和,考查了对数性质的应用,是中档题.

练习册系列答案
相关题目
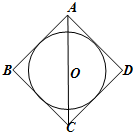 如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,在正方形ABCD内作内切圆O,将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )A、2:
| ||
B、2
| ||
C、2:
| ||
D、
|
圆锥的底面半径为1,母线长为3,则圆锥的表面积为( )
| A、π | B、2π | C、3π | D、4π |
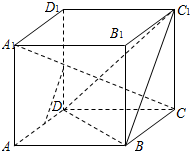 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;
如图,在正方体ABCD-A1B1C1D1中,E,F分别是AD,DD1中点.求证:(1)EF∥平面C1BD;