题目内容
6．已知f（x）在x0处可导，则$\underset{lim}{h→0}\frac{f（{x}_{0}+h）-f（{x}_{0}）}{2h}$等于（ ）| A． | $\frac{1}{2}f′（{x}_{0}）$ | B． | f′（x0） | C． | 2f′（x0） | D． | 4f′（x0） |
分析 把要求的式子变形为$\frac{1}{2}\lim_{h→0}\frac{f（{x}_{0}+h）-f（{x}_{0}）}{h}$，再利用函数在某一点的导数的定义得出结论．
解答 解：$\lim_{h→0}\frac{f（{x}_{0}+h）-f（{x}_{0}）}{2h}$=$\frac{1}{2}\lim_{h→0}\frac{f（{x}_{0}+h）-f（{x}_{0}）}{h}$=$\frac{1}{2}f′（{x}_{0}）$，
故选：A．
点评 本题主要考查函数在某一点的导数的定义，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
9．给定集合A={a1，a2，a3，…，an}（n∈N*?，n≥3），定义ai+aj（1≤i＜j≤n，i，j∈N*）中所有不同值的个数为集合A两元素和的容量，用L（A）表示，若A={2，4，6，8}，则L（A）=5；若集合A={a1，a2，a 3，…，a 100}，则L（A）的最小值为（ ）
| A． | 5050 | B． | 4950 | C． | 197 | D． | 195 |
10．一个几何体的三视图如图所示，该几何体的体积是（ ）
| A． | 12 | B． | 18 | C． | 24 | D． | 36 |
7．
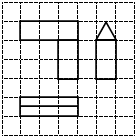如图，网格纸的小正方形的边长是1，粗线画出的是一个几何体的三视图，则这个几何体的体积为（ ）
如图，网格纸的小正方形的边长是1，粗线画出的是一个几何体的三视图，则这个几何体的体积为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{7}{2}$ | C． | 2+$\frac{\sqrt{3}}{4}$ | D． | 3+$\frac{\sqrt{3}}{3}$ |
18．已知$tanθ=\frac{3}{4}$，那么$tan（θ+\frac{π}{4}）$等于（ ）
| A． | -7 | B． | $-\frac{1}{7}$ | C． | 7 | D． | $\frac{1}{7}$ |
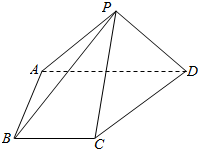如图，四棱锥P-ABCD中，平面PAD⊥底面ABCD，PA⊥PD，PA=PD，BC∥AD，AB⊥AD，AD=2AB=2BC=2．