题目内容
已知函数f(x)=
的定义域为D,集合A=[-π,π].
(Ⅰ)求D∩A;
(Ⅱ)若f(x)=
,求sin2x的值.
| cos2x | ||
sin(x+
|
(Ⅰ)求D∩A;
(Ⅱ)若f(x)=
| 4 |
| 3 |
考点:三角函数中的恒等变换应用
专题:函数的性质及应用
分析:(Ⅰ)首先,求解函数的定义域,然后,借助于集合的交集运算求解;
(Ⅱ)首先,利用f(x)=
,得到cosx-sinx=
,然后,借助于二倍角公式求解.
(Ⅱ)首先,利用f(x)=
| 4 |
| 3 |
2
| ||
| 3 |
解答:
解:(Ⅰ)由题意,sin(x+
)≠0,
∴x+
≠kπ(k∈Z),
则函数f(x)的定义域为D={x∈R|x≠kπ-
,k∈Z},
而A=[-π,π],
∴x≠-
,x≠
,
∴集合A∩D=[-π,-
)∪(-
,
)∪(
,π].
(Ⅱ)f(x)=
=
=
=
=
(cosx-sinx).
∵f(x)=
,
∴cosx-sinx=
.
∴sin2x=1-(cosx-sinx)2=1-
=
.
| π |
| 4 |
∴x+
| π |
| 4 |
则函数f(x)的定义域为D={x∈R|x≠kπ-
| π |
| 4 |
而A=[-π,π],
∴x≠-
| π |
| 4 |
| 3π |
| 4 |
∴集合A∩D=[-π,-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
(Ⅱ)f(x)=
| cos2x | ||
sin(x+
|
| cos2x | ||||
sinxcos
|
=
| ||
| sinx+cosx |
=
| ||
| sinx+cosx |
| 2 |
∵f(x)=
| 4 |
| 3 |
∴cosx-sinx=
2
| ||
| 3 |
∴sin2x=1-(cosx-sinx)2=1-
| 8 |
| 9 |
| 1 |
| 9 |
点评:本题重点考查了三角函数的图象与性质、二倍角公式、两角和与差的三角函数等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
向如图中所示正方形内随机地投掷飞镖,飞镖落在阴影部分的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=3,b=4,c=
,那么C等于( )
| 13 |
| A、30° | B、45° |
| C、60° | D、120° |
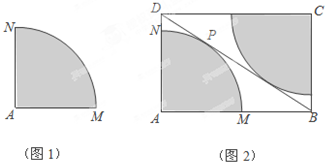 某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).
某中学校园内原有一块四分之一圆面形状的草坪AMN(图1),其中AM=AN=8m,∠MAN=90°.今年暑假整治校园环境时,为美观起见,学校设计将原有草坪扩大,具体实施方案是:从圆弧上一点P作圆弧的切线BD,分别与AM,AN的延长线交于B,D,并以AB,AD为邻边构造矩形ABCD,再以C为圆心制作一块与AMN形状相同的草坪,构成矩形绿地ABCD(图2).