题目内容
9.在平面直角坐标系xOy中,已知过点M(1,1)的直线l与圆(x+1)2+(y-2)2=5相切,且与直线ax+y-1=0垂直,则实数a=( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
分析 求出直线ax+y-1=0的斜率-a,判断点与圆的位置关系,然后列出方程,即可得出结论.
解答 解:由题意,点M(1,1)满足圆(x+1)2+(y-2)2=5的方程,
所以,点在圆上,圆的圆心(-1,2),
过点M(1,1)的直线l与圆(x+1)2+(y-2)2=5相切,且与直线ax+y-1=0垂直,
所以直线ax+y-1=0的斜率-a=$\frac{2-1}{-1-1}$=-$\frac{1}{2}$,
∴a=$\frac{1}{2}$.
故选:A.
点评 本题考查直线的斜率,考查直线与圆的位置关系,判断点与圆的位置关系是解题的关键,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.在正方形ABCD内随机生成n个点,其中在正方形ABCD内切圆内的点共有m个,利用随机模拟的方法,估计圆
周率π的近似值为( )
周率π的近似值为( )
| A. | $\frac{m}{n}$ | B. | $\frac{2m}{n}$ | C. | $\frac{4m}{n}$ | D. | $\frac{6m}{n}$ |
4.某市组织了一次高三调研考试,考后统计的数学成绩ξ-N(80,100),则下列说法中不正确的是( )
| A. | 该市这次考试的数学平均成绩为80分 | |
| B. | 分数在120分以上的人数与分数在60分以下的人数相同 | |
| C. | 分数在110以上的人数与分数在50分以下的人数相同 | |
| D. | 该市这次考试的数学成绩的标准差为10 |
 中,已知曲线
中,已知曲线 (
( 为参数),以平面直角坐标系
为参数),以平面直角坐标系 为极点,
为极点, 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 .
. 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 ,2倍后得到曲线
,2倍后得到曲线 ,试写出直线
,试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 ,使点
,使点 到直线
到直线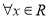 ,
, ;
; ”是假命题,则
”是假命题,则 都是假命题;
都是假命题; ”的否定是“
”的否定是“ ,
, ”
” ”是“函数
”是“函数 是在
是在 上的单调函数”的( )
上的单调函数”的( )