题目内容
14.已知数列{an}为公差不为0的等差数列,满足a1+a2+a3=21,且a1,a6,a21成等比数列.(1)求{an}的通项公式;
(2)若数列{bn}满足$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=an(n∈N*),且b1=$\frac{1}{3}$,求数列{bn}的前n项和Tn.
分析 (1)设数列{an}的公差为d,运用等差数列的通项公式和等比数列中项的性质,列方程,解方程即可得到首项和公差,进而得到所求通项公式;
(2)运用当n≥2时,$\frac{1}{{b}_{n}}$=($\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n-1}}$)+($\frac{1}{{b}_{n-1}}$-$\frac{1}{{b}_{n-2}}$)+…+($\frac{1}{{b}_{2}}$-$\frac{1}{{b}_{1}}$)+$\frac{1}{{b}_{1}}$,结合等差数列的求和公式,化简可得$\frac{1}{{b}_{n}}$=n(n+2),bn=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),再由数列的求和方法:裂项相消求和,化简整理即可得到所求和.
解答 解:(1)设数列{an}的公差为d,
由a1+a2+a3=21,且a1,a6,a21成等比数列.
可得$\left\{\begin{array}{l}{3{a}_{1}+3d=21}\\{{a}_{1}({a}_{1}+20d)=({a}_{1}+5d)^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=5}\\{d=2}\end{array}\right.$,
∴an=a1+(n-1)d=2n+3,n∈N*.
(2)由$\frac{1}{{b}_{n+1}}$-$\frac{1}{{b}_{n}}$=an(n∈N*),
∴$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n-1}}$=an-1(n≥2,n∈N*),
当n≥2时,$\frac{1}{{b}_{n}}$=($\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n-1}}$)+($\frac{1}{{b}_{n-1}}$-$\frac{1}{{b}_{n-2}}$)+…+($\frac{1}{{b}_{2}}$-$\frac{1}{{b}_{1}}$)+$\frac{1}{{b}_{1}}$
=an-1+an-2+…+a1+$\frac{1}{{b}_{1}}$=(2n+1)+(2n-1)+…+5+3=$\frac{1}{2}$(n-1)(2n+6)+3=n(n+2),
对b1=$\frac{1}{3}$上式也成立,
∴$\frac{1}{{b}_{n}}$=n(n+2),
∴bn=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴前n项和Tn=$\frac{1}{2}$[1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$($\frac{3}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)=$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$.
点评 本题考查等差数列的通项公式和求和公式的运用,考查等比数列中项的性质,以及数列的恒等式,数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图所示的三角形数:将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:b2017是数列{an}中的第5044项.
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图所示的三角形数:将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn},可以推测:b2017是数列{an}中的第5044项. .
. ;
; ,求证:
,求证: ,
, 恒成立.
恒成立. 的定义域是_________.
的定义域是_________. :实数
:实数 满足不等式
满足不等式 ,
, :函数
:函数 无极值点.
无极值点. ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数 的取值范围;
的取值范围; ,且
,且 :
: ,若
,若 是
是 的必要不充分条件,求正整数
的必要不充分条件,求正整数 的值.
的值. 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, ,
, .
.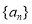 ,
, 的通项公式;
的通项公式; 的前
的前 项和
项和 .
.