题目内容
5.在△ABC中,角A,B,C所对的边分别为a,b,c,A=2C,且$cosA=\frac{1}{3}$(Ⅰ)求cosC的值;
(Ⅱ)若△ABC的面积为$5\sqrt{2}$,求sinB及边b.
分析 (I)使用二倍角公式得出关于cosC的方程解出;
(II)使用和角公式计算sinB,利用正弦定理和面积公式计算b.
解答 解:(I)∵cosA=cos2C=2cos2C-1=$\frac{1}{3}$,∴cosC=±$\frac{\sqrt{6}}{3}$.
∵A=2C,∴C是锐角,
∴cosC=$\frac{\sqrt{6}}{3}$.
(II)∵cosA=$\frac{1}{3}$,cosC=$\frac{\sqrt{6}}{3}$,
∴sinA=$\frac{2\sqrt{2}}{3}$,sinC=$\frac{\sqrt{3}}{3}$.
∴sinB=sin(A+C)=sinAcosC+cosAsinC=$\frac{5\sqrt{3}}{9}$.
由正弦定理得$\frac{a}{b}=\frac{sinA}{sinB}=\frac{2\sqrt{6}}{5}$.∴a=$\frac{2\sqrt{6}}{5}b$
∵S△ABC=$\frac{1}{2}absinC=\frac{1}{2}×\frac{2\sqrt{6}}{5}{b}^{2}×\frac{\sqrt{3}}{3}$=5$\sqrt{2}$,
∴b=5.
点评 本题考查了三角函数的恒等变换,利用正弦定理解三角形,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,-3).若向量$\overrightarrow{c}$满足$\overrightarrow{c}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),且$\overrightarrow{b}$∥($\overrightarrow{a}$-$\overrightarrow{c}$),则$\overrightarrow{c}$=( )
| A. | $(\frac{7}{9},\frac{7}{3})$ | B. | $(-\frac{7}{9},\frac{7}{3})$ | C. | $(\frac{7}{9},-\frac{7}{3})$ | D. | $(-\frac{7}{9},-\frac{7}{3})$ |
16.调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
(Ⅰ)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(Ⅱ)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m-n,求随机变量ξ的分布列及其数学期望.
10.若双曲线的顶点和焦点分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的焦点和顶点,则该双曲线方程为( )
| A. | x2-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
14.若f(x)=xex-a有两个零点,则实数a的取值范围是( )
| A. | ($\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$) | C. | (-$\frac{1}{e}$,+∞) | D. | (-$\frac{1}{e}$,0) |
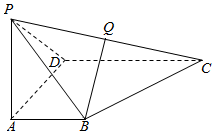 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.