题目内容
在(2x+
)4的二项展开式中,含x3项的系数是 .
| 3 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得常数项展开式中x3的系数.
解答:
解:(2x+
)4的二项展开式的通项公式为Tr+1=
•3
•24-r•x4-r,
令4-r=3,求得r=1,
∴含x3项的系数是
•
•8=32
,
故答案为:32
.
| 3 |
| C | r 4 |
| r |
| 2 |
令4-r=3,求得r=1,
∴含x3项的系数是
| C | 1 4 |
| 3 |
| 3 |
故答案为:32
| 3 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
若
=1-bi,(其中a,b都是实数,i是虚数单位),则|a+bi|=( )
| a |
| 1-i |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
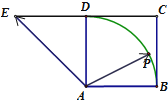 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量