题目内容
19.已知O是边长为2的等边△ABC的重心,则 ($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)=-$\frac{2}{3}$.分析 由已知得OA,OB,OC两两夹角为120°,|OA|=|OB|=|OC|=$\frac{2\sqrt{3}}{3}$,从而$\overrightarrow{OA}•\overrightarrow{OC}$=$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}$=-$\frac{2}{3}$,由此能求出($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)的值.
解答 解:∵O是边长为2的等边△ABC的重心,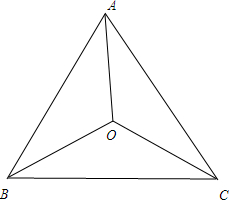
∴OA,OB,OC两两夹角为120°,
|OA|=|OB|=|OC|=$\frac{2}{3}\sqrt{4-1}$=$\frac{2\sqrt{3}}{3}$,
$\overrightarrow{OA}•\overrightarrow{OC}$=|$\overrightarrow{OA}$|•|$\overrightarrow{OC}$|•cos120°=$\frac{4}{3}•(-\frac{1}{2})=-\frac{2}{3}$,
同理,$\overrightarrow{OA}•\overrightarrow{OB}=\overrightarrow{OB}•\overrightarrow{OC}$=-$\frac{2}{3}$,
($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)
=$\overrightarrow{OA}$2+$\overrightarrow{OA}•\overrightarrow{OC}$+$\overrightarrow{OA}•\overrightarrow{OB}$+$\overrightarrow{OB}•\overrightarrow{OC}$
=$\frac{4}{3}-\frac{2}{3}-\frac{2}{3}-\frac{2}{3}$=-$\frac{2}{3}$.
故答案为:$-\frac{2}{3}$.
点评 本题考查平面向量数量积、三角形重心性质等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、函数与方程思想,是中档题.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 30° | B. | 45° | C. | 135° | D. | 45°或135° |
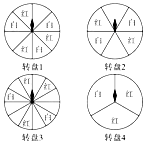 如图,是四个可以自由转动的转盘,转盘被平均分成若干个扇形,转动转盘,转盘停止后,有两个转盘的指针指向白色区域的概率相同,则这两个转盘是( )
如图,是四个可以自由转动的转盘,转盘被平均分成若干个扇形,转动转盘,转盘停止后,有两个转盘的指针指向白色区域的概率相同,则这两个转盘是( )| A. | 转盘1和转盘2 | B. | 转盘2和转盘3 | C. | 转盘2和转盘4 | D. | 转盘3和转盘4 |
| A. | -6 | B. | -3 | C. | -2 | D. | 6 |