题目内容

16．方程x2-2x+m=0在（-1，5）有一根，实数m的取值范围为-15＜m≤-3或m=1．

分析 由x2-2x+m=0（-1＜x＜5）分离参数m得：m=2x-x2=-（x-1）2+1（-1＜x＜5），作出图形，利用二次函数的性质可得答案．

解答 解：由x2-2x+m=0（-1＜x＜5）得：m=2x-x2=-（x-1）2+1（-1＜x＜5），
作图如下：

由图可知，当-15＜m≤-3或m=1时，
直线y=m与曲线y=-（x-1）2+1（-1＜x＜5）只有一个交点，
即方程x2-2x+m=0在（-1，5）有一根，
故答案为：-15＜m≤-3或m=1．

点评 本题考查函数的零点与根的分布，分离参数是关键，考查等价转化思想与数形结合思想的综合运用，属于中档题．

练习册系列答案
相关题目
6．若a1＞0，a1≠1，an+1=$\frac{2{a}_{n}}{1+{a}_{n}}$（n=1，2，…）．
（1）求证：an+1≠an；
（2）令a1=$\frac{1}{2}$，写出a2，a3，a4，a5的值，观察并归纳出这个数列的通项公式an，并用数学归纳法证明．
7．已知函数f（x）=$\frac{{2}^{x}-a•{2}^{x}}{{2}^{x}+{2}^{-x}}$是定义R在上的奇函数．
（1）求实数a的值，并求函数f（x）的值域；
（2）设g（x）=（2x+2-x）•f（x）．
（ⅰ）判断函数y=g（x）的单调性（不需要说明理由），并求使不等式g（x2+tx）+g（4-x）＞0对x∈R恒成立的实数t的取值范围；
（ⅱ）设h（x）=22x+2-2x-2m•g（x）且h（x）在[1，+∞）上的最小值为-2，求实数m的值．
4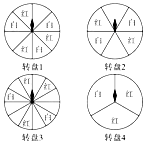．如图，是四个可以自由转动的转盘，转盘被平均分成若干个扇形，转动转盘，转盘停止后，有两个转盘的指针指向白色区域的概率相同，则这两个转盘是（　　）
A．转盘1和转盘2B．转盘2和转盘3C．转盘2和转盘4D．转盘3和转盘4
11．设f（x）为定义在R上的奇函数，当x≥0时，f（x）=3x+1-3，则f（-1）的值为（　　）
A．-6B．-3C．-2D．6
1．若向量$\overrightarrow{a}$、$\overrightarrow{b}$ 满足|$\overrightarrow{a}$|=$\sqrt{2}$，|$\overrightarrow{b}$|=1，$\overrightarrow{a}•\overrightarrow{b}$=-1，则向量$\overrightarrow{a}$、$\overrightarrow{b}$ 的夹角的大小为$\frac{3π}{4}$．
8．在等腰△ABC中，A=120°，则向量$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为150°．
5．从一个含有40个个体的总体中抽取一个容量为7的样本，将个体依次随机编号为01，02，…，40，从随机数表的第6行第8列开始，依次向右，到最后一列转下一行最左一列开始，直到取足样本，则获取的第4个样本编号为06（下面是随机数表第6行和第7行）
第6行84 42 17 56 31 07 23 55 06 82 77  04 74 43 59 76 30 63 50 25 83 92 12 06
第7行63 01  63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38．
20．（x-a）10的展开式中，x7的系数为15，则实数a=（　　）
A．$-\frac{1}{2}$B．$\frac{1}{2}$C．$-\frac{1}{8}$D．$\frac{1}{8}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网