题目内容
9.定义f(n)=$\sum_{i=1}^{n}$[$\frac{n}{i}$],其中[x]表示不超过实数x的最大整数,则f(2010)-f(2009)=16.分析 利用性质:由于2010=1×2×3×5×67,2009=1×7×7×41,可得:$[\frac{2010}{i}]$-$[\frac{2009}{i}]$=f(i),i∈{1,2,…,2009}.当i=1,2,3,5,67,6,10,134,15,191,335,30,402,670,1005时,f(i)=1;当i取其它值时,f(i)=0.
解答 解:f(2010)-f(2009)=$[\frac{2010}{1}]$+$[\frac{2010}{2}]$+…+$[\frac{2010}{2008}]$+$[\frac{2010}{2009}]$+$[\frac{2010}{2010}]$-($[\frac{2009}{1}]$+$[\frac{2009}{2}]$+…+$[\frac{2009}{502}]$+$[\frac{2009}{503}]$+…+$[\frac{2009}{669}]$+…+$[\frac{2009}{1004}]$+$[\frac{2009}{1005}]$+…+$[\frac{2009}{2008}]$+$[\frac{2009}{2009}]$),
利用性质:由于2010=1×2×3×5×67,2009=1×7×7×41,
可得:$[\frac{2010}{i}]$-$[\frac{2009}{i}]$=f(i),i∈{1,2,…,2009}.
①当i=1,2,3,5,67,6,10,134,15,191,335,30,402,670,1005时,f(i)=1;
②当i取其它值时,f(i)=0.
∴f(2010)-f(2009)=15+$[\frac{2010}{2010}]$=16,
故答案为:16.
点评 本题考查了高斯函数[x]的性质、分类讨论方法、数的分解,考查了推理能力与计算能力,属于难题.

| A. | (-1,2] | B. | (0,2) | C. | (0,2] | D. | (1,+∞) |
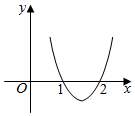 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.