题目内容
1.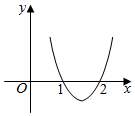 已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导导数y=f′(x)的图象经过点(1,0),(2,0),如图所示,求x0的值和函数(x)的极小值.
分析 观察图象满足f′(x)=0的点附近的导数的符号的变化情况,来确定极小值,求出x0的值;由函数的图象知函数在x=2处取得极小值.
解答 解:由图象可知,在(-∞,1)上f′(x)>0,在(1,2)上f′(x)<0.
在(2,+∞)上f′(x)>0.
故f(x)在(-∞,1),(2,+∞)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x0=1.
f′(x)=3ax2+2bx+c,
由f′(1)=0,f′(2)=0,f(1)=5,
得$\left\{\begin{array}{l}{3a+2b+c=0}\\{12a+4b+c=0}\\{a+b+c=5}\end{array}\right.$,
解得a=2,b=-9,c=12;
可得函数在x=2处取得极小值f(2)=2×23-9×22+24=4.
点评 本题主要考查了利用导数研究函数的极值、单调性,以及观察图形的能力,属于中档题.

练习册系列答案
相关题目
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
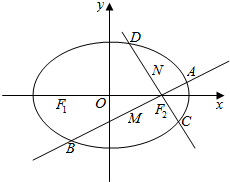 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.