题目内容
14.已知f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=$\frac{2}{x-2}$.求f(x)与g(x)的解析式.分析 将-x代入已知等式,利用函数f(x)、g(x)的奇偶性,得到关于f(x)与g(x)的又一个方程,将二者看做未知数解方程组,解得f(x)和g(x)的解析式.
解答 解:∵f(x)是偶函数,g(x)是奇函数,
∴g(-x)=-g(x),f(-x)=f(x),
令x取-x,代入f(x)+g(x)=$\frac{2}{2-x}$①,
可得f(-x)+g(-x)=$\frac{2}{2+x}$,
即f(x)-g(x)=f(-x)+g(-x)=$\frac{2}{2+x}$②,
由①②解得,f(x)=$\frac{4}{4-{x}^{2}}$,g(x)=$\frac{2x}{4-{x}^{2}}$.
点评 本题考查了函数奇偶性的性质的应用,以及列方程组法求函数的解析式.

练习册系列答案
相关题目
2.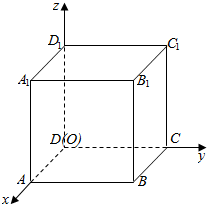 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )| A. | (1,$\sqrt{2}$,$\sqrt{2}$) | B. | (1,1,$\sqrt{2}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}$,1) |
6.“-$\sqrt{2}$≤k≤$\sqrt{2}$”是“直线x-y+k=0与圆x2+y2=1相交”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |