题目内容
方程
sinx-cosx=0(x∈[0,2π])的所有解之和为 .
| 3 |
考点:函数的零点
专题:函数的性质及应用
分析:由三角函数公式可得
sinx-cosx=2sin(x-
)=0,结合x∈[0,2π],可得x值,求和即可.
| 3 |
| π |
| 6 |
解答:
解:∵
sinx-cosx=0,
∴
sinx-
cosx=0
∴sin(x-
)=0
∴x-
=kπ,k∈Z,
∴x=kπ+
,k∈Z,
又∵x∈[0,2π],
∴x=
,x=
,
∴
+
=
故答案为:
.
| 3 |
∴
| ||
| 2 |
| 1 |
| 2 |
∴sin(x-
| π |
| 6 |
∴x-
| π |
| 6 |
∴x=kπ+
| π |
| 6 |
又∵x∈[0,2π],
∴x=
| π |
| 6 |
| 7π |
| 6 |
∴
| π |
| 6 |
| 7π |
| 6 |
| 4π |
| 3 |
故答案为:
| 4π |
| 3 |
点评:本题考查两角和与差的三角函数公式,属基础题.

练习册系列答案
相关题目
 如图,三棱柱ABC-A1B1C1中,CC1=BC1=
如图,三棱柱ABC-A1B1C1中,CC1=BC1=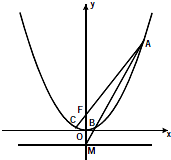 已知抛物线C:x2=2py(p>0)上纵坐标为p的点到焦点F的距离为3.
已知抛物线C:x2=2py(p>0)上纵坐标为p的点到焦点F的距离为3.