题目内容
18．已知集合A={x∈R|x2-4x＜0}，B={x∈R|2x＜8}，则A∩B=（ ）| A． | （0，3） | B． | （3，4） | C． | （0，4） | D． | （-∞，3） |
分析 先分别求出集体合A和B，由此能求出A∩B．
解答 解：∵集合A={x∈R|x2-4x＜0}={x|0＜x＜4}，
B={x∈R|2x＜8}={x|x＜3}，
∴A∩B={x|0＜x＜3}=（0，3）．
故选：A．
点评 本题考查交集的求法，是基础题，解题时要 认真审题，注意交集定义的合理运用．
练习册系列答案
相关题目
8．已知集合A={x|$\frac{x+1}{x-2}$＜0}，集合B=N，则A∩B=（ ）
| A． | {-1，0，1} | B． | {1} | C． | {0，1} | D． | {-1，0} |
6．若a，b，c∈R，则下列说法正确的是（ ）
| A． | 若a＞b，则a-c＞b-c | B． | 若a＞b，则$\frac{1}{a}＜\frac{1}{b}$ | C． | 若a＞b，则a2＞b2 | D． | 若a＞b，则ac2＞bc2 |
13．
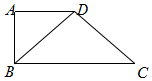如图所示，四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将
△ABD沿BD折起，使面ABD⊥面BCD，连结AC，则下列命题正确的是（ ）
如图所示，四边形ABCD中，AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿BD折起，使面ABD⊥面BCD，连结AC，则下列命题正确的是（ ）
| A． | 面ABD⊥面ABC | B． | 面ADC⊥面BDC | C． | 面ABC⊥面BDC | D． | 面ADC⊥面ABC |
3．函数f（x）=|sinx+cosx|+|sinx-cosx|是（ ）
| A． | 最小正周期为π的奇函数 | B． | 最小正周期为π的偶函数 | ||
| C． | 最小正周期为$\frac{π}{2}$的奇函数 | D． | 最小正周期为$\frac{π}{2}$的偶函数 |
10．已知全集U={1，2，3，4}，集合A={1，2}，集合B={2，3}，则∁U（A∪B）=（ ）
| A． | {4} | B． | {3} | C． | {1，3，4} | D． | {3，4} |