题目内容
2.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)以椭圆C2:$\frac{{x}^{2}}{{m}^{2}}+\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)的焦点F1,F2为顶点,且以椭圆C2的右顶点A为一个焦点,它的一条渐近线与椭圆C2交于P,Q,若$\overrightarrow{AP}•\overrightarrow{PQ}$=0,则双曲线C1的离心率e满足( )| A. | e2=$\frac{\sqrt{2}+1}{2}$ | B. | e2=$\frac{\sqrt{3}+1}{2}$ | C. | e2=$\frac{3}{2}$ | D. | e2=$\frac{\sqrt{5}+1}{2}$ |
分析 由条件可得a2=m2-n2,m2=a2+b2,可得n2=b2,将椭圆方程化为b2x2+c2y2=b2c2,求出双曲线的一条渐近线方程代入椭圆方程,求得P的坐标,又A(c,0),由向量垂直的条件,即两直线垂直的条件:斜率之积为-1,化简整理,结合离心率公式和a,b,c的关系,可得e的方程,解方程即可得到所求值.
解答 解:由题意可得a2=m2-n2,m2=a2+b2,
可得n2=b2,
则椭圆方程化为b2x2+(a2+b2)y2=b2(a2+b2),
即b2x2+c2y2=b2c2,
由双曲线的一条渐近线方程y=$\frac{b}{a}$x,代入椭圆方程可得,
(b2+c2•$\frac{{b}^{2}}{{a}^{2}}$)x2=b2c2,
解得x=±$\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}$,
可取P($\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}$,$\frac{bc}{\sqrt{{a}^{2}+{c}^{2}}}$),又A(c,0),
若$\overrightarrow{AP}•\overrightarrow{PQ}$=0,则$\overrightarrow{AP}$⊥$\overrightarrow{PQ}$,
可得kAP=-$\frac{a}{b}$,
即为$\frac{\frac{bc}{\sqrt{{a}^{2}+{c}^{2}}}}{\frac{ac}{\sqrt{{a}^{2}+{c}^{2}}}-c}$=-$\frac{a}{b}$,
化为c2=a$\sqrt{{a}^{2}+{c}^{2}}$,
两边平方可得c4=a4+a2c2,
两边同除以a4,结合e=$\frac{c}{a}$,可得
e4-e2-1=0,
解得e2=$\frac{\sqrt{5}+1}{2}$(负的舍去).
故选:D.
点评 本题考查椭圆和双曲线的方程和性质,主要是渐近线方程和离心率求法,注意运用方程思想,考查化简整理的运算能力,属于中档题.

| A. | 直线x=1对称 | B. | 直线x=-1对称 | C. | 点(1,0)对称 | D. | 点(-1,0)对称 |
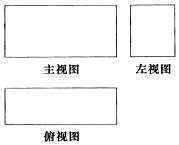 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )| A. | 3$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 6$\sqrt{5}$+4 | D. | 10 |
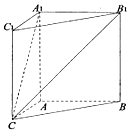 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.