题目内容
已知函数f(x)=
,则“-
≤a≤0”是“f(x)在R上单调递增”的( )
|
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:当a=0时,f(x)=
,在R上单调递增.当a≠0时,f(x)在R上单调递增,利用二次函数与一次函数的单调性可得
,解出即可.
|
|
解答:
解:当a=0时,f(x)=
,在R上单调递增.
当a≠0时,f(x)在R上单调递增,
,解得-
≤a<0.
综上可得:“-
≤a≤0”?“f(x)在R上单调递增”.
故选:C.
|
当a≠0时,f(x)在R上单调递增,
|
| 1 |
| 2 |
综上可得:“-
| 1 |
| 2 |
故选:C.
点评:本题考查了一次函数与二次函数的单调性、分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
要得到函数y=-sin2x+
的图象,只需将y=sinxcosx的图象( )
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设f1(x)=cosx,定义fn+1(x)为fn(x)的导数,即fn+1(x)=fn′(x),n∈N+,若△ABC的内角A满足f1(A)+f2(A)+…+f2014(A)=0,则sinA的值是( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
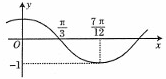 函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
若
、
、
三个单位向量两两之间夹角为60°,则|
+
+
|=( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| A、3 | ||
B、
| ||
| C、6 | ||
D、
|