题目内容
19.已知不等式kx2-2x+6k<0 (k≠0),若不等式的解集为∅,则k的取值范围为k≥$\frac{\sqrt{6}}{6}$.分析 根据题意,得出不等式组$\left\{\begin{array}{l}{k>0}\\{△≤0}\end{array}\right.$,求出解集即可.
解答 解:∵不等式kx2-2x+6k<0 (k≠0)的解集为∅,
∴应满足$\left\{\begin{array}{l}{k>0}\\{△≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{k>0}\\{4-2{4k}^{2}≤0}\end{array}\right.$;
解得$\left\{\begin{array}{l}{k>0}\\{k≥\frac{\sqrt{6}}{6}或k≤-\frac{\sqrt{6}}{6}}\end{array}\right.$,
∴k的取值范围是k≥$\frac{\sqrt{6}}{6}$.
故答案为:k≥$\frac{\sqrt{6}}{6}$.
点评 本题考查一元二次不等式与二次函数的应用问题,也考查了判别式的应用问题,是基础题目.

练习册系列答案
相关题目
7.下列条件能唯一确定一个平面的是( )
| A. | 空间任意三点 | B. | 不共线三点 | C. | 共线三点 | D. | 两条异面直线 |
4.已知A(1,0)、B(2,-1),若点P(x,y)满足x+y+1=0,则|PA|+|PB|的最小值为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
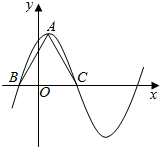 函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象
函数f(x)=3cos2$\frac{ωx}{2}$+$\frac{\sqrt{3}}{2}$sinωx-$\frac{3}{2}$(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为等边三角形.将函数f(x)的图象上各点的横坐标变为原来的π倍,将所得图象向右平移$\frac{2π}{3}$个单位,再向上平移1个单位,得到函数y=g(x)的图象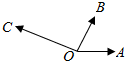 如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )
如图所示,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,|$\overrightarrow{OC}$|=$\sqrt{3}$,∠AOB=60°,$\overrightarrow{OB}$⊥$\overrightarrow{OC}$.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则x,y的值分别是( )