题目内容
3.已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在函数y=x2-10x的图象上,等差数列{bn}满足bn+bn+1=an(n∈N*),其前n项和为Tn,则下列结论正确的是( )| A. | Sn<2Tn | B. | b4=0 | C. | T7>b7 | D. | T5=T6 |
分析 先求出${S}_{n}={n}^{2}-10n$,从而an=2n-11.由等差数列{bn}满足bn+bn+1=an(n∈N*),求出{bn}是公差d=1,首项b1=-5的等差数列,由此能求出结果.
解答 解:∵数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在函数y=x2-10x的图象上,
∴${S}_{n}={n}^{2}-10n$,
∴a1=1-10=-9,
an=Sn-Sn-1=(n2-10n)-[(n-1)2-10(n-1)]=2n-11,(n≥2)
当n=1时,an=2-11=-9=a1,
∴an=2n-11.
∵等差数列{bn}满足bn+bn+1=an(n∈N*),
∴b1+b2=-9,b2+b3=a2=4-11=-7,
(b2+b3)-(b1+b2)=b3-b1=2d=-7+9=2,
∴d=1,b1=-5,
∴Tn=-5n+$\frac{n(n-1)}{2}×1$=$\frac{{n}^{2}-11n}{2}$.
在A 中,Sn-2Tn=(n2-10n)-(n2-11n)=n>0,∴Sn>2Tn,故A错误;
在B中,b4=-5+3×1=-2,故B错误;
在C中,T7-b7=[7×(-5)+$\frac{7×6}{2}×1$]-(-5+6)=-14-1=-15<0,
∴T7<b7,故C错误;
在D中,T5-T6=[5×(-5)+$\frac{5×4}{2}×1$]-[6×(-5)-$\frac{6×5}{2}×1$]=0,
∴T5=T6,故D正确.
故选:D.
点评 本题考查命题真假的判断,涉及到函数性质、等差数列等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
13.“=”在基本算法语句中叫( )
| A. | 赋值号 | B. | 等号 | C. | 输入语句 | D. | 输出语句 |
15.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,M(x0,y0)(x0>0,y0>0)是双曲线的渐近线上一点,满足MF1⊥MF2,如果以F2为焦点的抛物线y2=2px(p>0)经过点M,则此双曲线的离心率为( )
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
12.某高校大一新生的五名同学打算参加学校组织的“小草文学社”、“街舞俱乐部”、“足球之家”、“骑行者”四个社团.若毎个社团至少一名同学参加,每名同学至少参加一个社团且只能参加一个社团,其中同学甲不参加“街舞俱乐部”,则这五名同学不同的参加方法的种数为( )
| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
6.有4个不同的球,四个不同的盒子,把球全部放入盒内,恰有两个盒不放球,共有( )种放法.
| A. | 114 | B. | 96 | C. | 84 | D. | 48 |
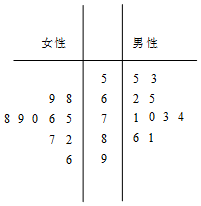 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示: