题目内容
9.不等式3x-5>5x+3的解集{x|x<-4};不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8>4x-1}\end{array}\right.$的整数解是1和2.分析 利用移项,通分,转化不等式求解即可.不等式组求解他们的交集.
解答 解:不等式3x-5>5x+3,
可得:-8>2x,
∴x<-4.
故得原不等式的解集为{x|x<-4}.
故答案为:{x|x<-4}.
不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8>4x-1}\end{array}\right.$,
由x-1≥1-x,解得:x≥1.
由x+8>4x-1,解得:x<3.
故得原不等式的解集为{x|1≤x<3}.
故答案为:1和2.
点评 本题考查不等式组的解法,基本知识的考查.

练习册系列答案
相关题目
20. 《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )
《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )
 《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )
《周髀算经》记载了勾股定理的公式与证明,勾股定理相传由商高(商代)发现,故又有称之为商高定理,满足等式a2+b2=c2的正整数组(a,b,c)叫勾股数,如(3,4,5)就是勾股数,执行如图所示的程序框图,如果输入的数是互相不相等的正整数,则下面四个结论正确的是( )| A. | 输出的数组都是勾股数 | B. | 任意正整数都是勾股数组中的一个 | ||
| C. | 相异两正整数都可以构造出勾股数 | D. | 输出的结果中一定有a<b<c |
14.若a>b,则下列不等式中正确的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a2>b2 | C. | a+b≥2$\sqrt{ab}$ | D. | a2+b2>2ab |
1.一个球的内接正方体的表面积为54,则球的表面积为 ( )
| A. | 27π | B. | 18π | C. | 9π | D. | 54π |
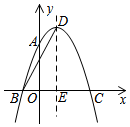 如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.
如图,抛物线y=ax2+2x+c经过点A(0,3),B(-1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:y=-x2+2x+3BD的长为2$\sqrt{5}$.